|
1 | 1 | # Polynomials.jl |
2 | 2 |
|
3 | | -Basic arithmetic, integration, differentiation, evaluation, and root finding over dense univariate [polynomials](https://en.wikipedia.org/wiki/Polynomial). |
| 3 | +Basic arithmetic, integration, differentiation, evaluation, root finding, and fitting for |
| 4 | +univariate [polynomials](https://en.wikipedia.org/wiki/Polynomial) in [Julia](https://julialang.org/). |
4 | 5 |
|
5 | 6 | [](https://JuliaMath.github.io/Polynomials.jl/stable) |
6 | 7 | [](https://github.com/JuliaMath/Polynomials.jl/actions/workflows/ci.yml) |
7 | 8 | [](https://codecov.io/gh/JuliaMath/Polynomials.jl) |
8 | | - |
9 | | - |
10 | | -## Installation |
11 | | - |
12 | | -```julia |
13 | | -(v1.6) pkg> add Polynomials |
14 | | -``` |
15 | | - |
16 | | -This package supports Julia v1.6 and later. |
17 | | - |
18 | | -## Available Types of Polynomials |
19 | | - |
20 | | -* `Polynomial` – standard basis polynomials, $a(x) = a_0 + a_1 x + a_2 x^2 + … + a_n x^n$ for $n ≥ 0$. |
21 | | -* `ImmutablePolynomial` – standard basis polynomials backed by a [Tuple type](https://docs.julialang.org/en/v1/manual/functions/#Tuples-1) for faster evaluation of values |
22 | | -* `SparsePolynomial` – standard basis polynomial backed by a [dictionary](https://docs.julialang.org/en/v1/base/collections/#Dictionaries-1) to hold sparse high-degree polynomials |
23 | | -* `LaurentPolynomial` – [Laurent polynomials](https://docs.julialang.org/en/v1/base/collections/#Dictionaries-1), $a(x) = a_m x^m + … + a_n x^n$ for $m ≤ n$ and $m,n ∈ ℤ$. This is backed by an [offset array](https://github.com/JuliaArrays/OffsetArrays.jl); for example, if $m<0$ and $n>0$, we obtain $a(x) = a_m x^m + … + a_{-1} x^{-1} + a_0 + a_1 x + … + a_n x^n$ |
24 | | -* `FactoredPolynomial` – standard basis polynomials, storing the roots, with multiplicity, and leading coefficient of a polynomial |
25 | | -* `ChebyshevT` – [Chebyshev polynomials](https://en.wikipedia.org/wiki/Chebyshev_polynomials) of the first kind |
26 | | -* `RationalFunction` - a type for ratios of polynomials. |
27 | | - |
28 | | -## Usage |
29 | | - |
30 | | -```julia |
31 | | -julia> using Polynomials |
32 | | -``` |
33 | | - |
34 | | -### Construction and Evaluation |
35 | | - |
36 | | -Construct a polynomial from an array (a vector) of its coefficients, lowest order first. |
37 | | - |
38 | | -```julia |
39 | | -julia> Polynomial([1,0,3,4]) |
40 | | -Polynomial(1 + 3*x^2 + 4*x^3) |
41 | | -``` |
42 | | - |
43 | | -Optionally, the variable of the polynomial can be specified. |
44 | | - |
45 | | -```julia |
46 | | -julia> Polynomial([1,2,3], :s) |
47 | | -Polynomial(1 + 2*s + 3*s^2) |
48 | | -``` |
49 | | - |
50 | | -Construct a polynomial from its roots. |
51 | | - |
52 | | -```julia |
53 | | -julia> fromroots([1,2,3]) # (x-1)*(x-2)*(x-3) |
54 | | -Polynomial(-6 + 11*x - 6*x^2 + x^3) |
55 | | -``` |
56 | | - |
57 | | -Evaluate the polynomial `p` at `x`. |
58 | | - |
59 | | -```julia |
60 | | -julia> p = Polynomial([1, 0, -1]); |
61 | | -julia> p(0.1) |
62 | | -0.99 |
63 | | -``` |
64 | | - |
65 | | -### Arithmetic |
66 | | - |
67 | | -Methods are added to the usual arithmetic operators so that they work on polynomials, and combinations of polynomials and scalars. |
68 | | - |
69 | | -```julia |
70 | | -julia> p = Polynomial([1,2]) |
71 | | -Polynomial(1 + 2*x) |
72 | | - |
73 | | -julia> q = Polynomial([1, 0, -1]) |
74 | | -Polynomial(1 - x^2) |
75 | | - |
76 | | -julia> p - q |
77 | | -Polynomial(2*x + x^2) |
78 | | - |
79 | | -julia> p = Polynomial([1,2]) |
80 | | -Polynomial(1 + 2*x) |
81 | | - |
82 | | -julia> q = Polynomial([1, 0, -1]) |
83 | | -Polynomial(1 - x^2) |
84 | | - |
85 | | -julia> 2p |
86 | | -Polynomial(2 + 4*x) |
87 | | - |
88 | | -julia> 2+p |
89 | | -Polynomial(3 + 2*x) |
90 | | - |
91 | | -julia> p - q |
92 | | -Polynomial(2*x + x^2) |
93 | | - |
94 | | -julia> p * q |
95 | | -Polynomial(1 + 2*x - x^2 - 2*x^3) |
96 | | - |
97 | | -julia> q / 2 |
98 | | -Polynomial(0.5 - 0.5*x^2) |
99 | | - |
100 | | -julia> q ÷ p # `div`, also `rem` and `divrem` |
101 | | -Polynomial(0.25 - 0.5*x) |
102 | | -``` |
103 | | - |
104 | | -Most operations involving polynomials with different variables will error. |
105 | | - |
106 | | -```julia |
107 | | -julia> p = Polynomial([1, 2, 3], :x); |
108 | | -julia> q = Polynomial([1, 2, 3], :s); |
109 | | -julia> p + q |
110 | | -ERROR: ArgumentError: Polynomials have different indeterminates |
111 | | -``` |
112 | | - |
113 | | -#### Construction and Evaluation |
114 | | - |
115 | | -While polynomials of type `Polynomial` are mutable objects, operations such as |
116 | | -`+`, `-`, `*`, always create new polynomials without modifying its arguments. |
117 | | -The time needed for these allocations and copies of the polynomial coefficients |
118 | | -may be noticeable in some use cases. This is amplified when the coefficients |
119 | | -are for instance `BigInt` or `BigFloat` which are mutable themselves. |
120 | | -This can be avoided by modifying existing polynomials to contain the result |
121 | | -of the operation using the [MutableArithmetics (MA) API](https://github.com/jump-dev/MutableArithmetics.jl). |
122 | | - |
123 | | -Consider for instance the following arrays of polynomials |
124 | | -```julia |
125 | | -using Polynomials |
126 | | -d, m, n = 30, 20, 20 |
127 | | -p(d) = Polynomial(big.(1:d)) |
128 | | -A = [p(d) for i in 1:m, j in 1:n] |
129 | | -b = [p(d) for i in 1:n] |
130 | | -``` |
131 | | - |
132 | | -In this case, the arrays are mutable objects for which the elements are mutable |
133 | | -polynomials which have mutable coefficients (`BigInt`s). |
134 | | -These three nested levels of mutable objects communicate with the MA |
135 | | -API in order to reduce allocation. |
136 | | -Calling `A * b` requires approximately 40 MiB due to 2 M allocations |
137 | | -as it does not exploit any mutability. |
138 | | - |
139 | | -Using |
140 | | - |
141 | | -```julia |
142 | | -using PolynomialsMutableArithmetics |
143 | | -``` |
144 | | - |
145 | | -to register `Polynomials` with `MutableArithmetics`, then multiplying with: |
146 | | - |
147 | | -```julia |
148 | | -using MutableArithmetics |
149 | | -const MA = MutableArithmetics |
150 | | -MA.operate(*, A, b) |
151 | | -``` |
152 | | - |
153 | | -exploits the mutability and hence only allocates approximately 70 KiB due to 4 k |
154 | | -allocations. |
155 | | - |
156 | | -If the resulting vector is already allocated, e.g., |
157 | | - |
158 | | -```julia |
159 | | -z(d) = Polynomial([zero(BigInt) for i in 1:d]) |
160 | | -c = [z(2d - 1) for i in 1:m] |
161 | | -``` |
162 | | - |
163 | | -then we can exploit its mutability with |
164 | | - |
165 | | -```julia |
166 | | -MA.operate!(MA.add_mul, c, A, b) |
167 | | -``` |
168 | | - |
169 | | -to reduce the allocation down to 48 bytes due to 3 allocations. |
170 | | - |
171 | | -These remaining allocations are due to the `BigInt` buffer used to |
172 | | -store the result of intermediate multiplications. This buffer can be |
173 | | -preallocated with: |
174 | | - |
175 | | -```julia |
176 | | -buffer = MA.buffer_for(MA.add_mul, typeof(c), typeof(A), typeof(b)) |
177 | | -MA.buffered_operate!(buffer, MA.add_mul, c, A, b) |
178 | | -``` |
179 | | - |
180 | | -then the second line is allocation-free. |
181 | | - |
182 | | -The `MA.@rewrite` macro rewrite an expression into an equivalent code that |
183 | | -exploit the mutability of the intermediate results. |
184 | | -For instance |
185 | | -```julia |
186 | | -MA.@rewrite(A1 * b1 + A2 * b2) |
187 | | -``` |
188 | | -is rewritten into |
189 | | -```julia |
190 | | -c = MA.operate!(MA.add_mul, MA.Zero(), A1, b1) |
191 | | -MA.operate!(MA.add_mul, c, A2, b2) |
192 | | -``` |
193 | | -which is equivalent to |
194 | | -```julia |
195 | | -c = MA.operate(*, A1, b1) |
196 | | -MA.mutable_operate!(MA.add_mul, c, A2, b2) |
197 | | -``` |
198 | | - |
199 | | -*Note that currently, only the `Polynomial` type implements the API and it only |
200 | | -implements part of it.* |
201 | | - |
202 | | -### Integrals and Derivatives |
203 | | - |
204 | | -Integrate the polynomial `p` term by term, optionally adding a constant |
205 | | -term `k`. The degree of the resulting polynomial is one higher than the |
206 | | -degree of `p` (for a nonzero polynomial). |
207 | | - |
208 | | -```julia |
209 | | -julia> integrate(Polynomial([1, 0, -1])) |
210 | | -Polynomial(1.0*x - 0.3333333333333333*x^3) |
211 | | - |
212 | | -julia> integrate(Polynomial([1, 0, -1]), 2) |
213 | | -Polynomial(2.0 + 1.0*x - 0.3333333333333333*x^3) |
214 | | -``` |
215 | | - |
216 | | -Differentiate the polynomial `p` term by term. For non-zero |
217 | | -polynomials the degree of the resulting polynomial is one lower than |
218 | | -the degree of `p`. |
219 | | - |
220 | | -```julia |
221 | | -julia> derivative(Polynomial([1, 3, -1])) |
222 | | -Polynomial(3 - 2*x) |
223 | | -``` |
224 | | - |
225 | | -### Root-finding |
226 | | - |
227 | | - |
228 | | -Return the roots (zeros) of `p`, with multiplicity. The number of |
229 | | -roots returned is equal to the degree of `p`. By design, this is not type-stable, the returned roots may be real or complex. |
230 | | - |
231 | | -```julia |
232 | | -julia> roots(Polynomial([1, 0, -1])) |
233 | | -2-element Vector{Float64}: |
234 | | - -1.0 |
235 | | - 1.0 |
236 | | - |
237 | | -julia> roots(Polynomial([1, 0, 1])) |
238 | | -2-element Vector{ComplexF64}: |
239 | | - 0.0 - 1.0im |
240 | | - 0.0 + 1.0im |
241 | | - |
242 | | -julia> roots(Polynomial([0, 0, 1])) |
243 | | -2-element Vector{Float64}: |
244 | | - 0.0 |
245 | | - 0.0 |
246 | | -``` |
247 | | - |
248 | | -### Fitting arbitrary data |
249 | | - |
250 | | -Fit a polynomial (of degree `deg` or less) to `x` and `y` using a least-squares approximation. |
251 | | - |
252 | | -```julia |
253 | | -julia> xs = 0:4; ys = @. exp(-xs) + sin(xs); |
254 | | - |
255 | | -julia> fit(xs, ys) |> p -> round.(coeffs(p), digits=4) |> Polynomial |
256 | | -Polynomial(1.0 + 0.0593*x + 0.3959*x^2 - 0.2846*x^3 + 0.0387*x^4) |
257 | | - |
258 | | -julia> fit(ChebyshevT, xs, ys, 2) |> p -> round.(coeffs(p), digits=4) |> ChebyshevT |
259 | | -ChebyshevT(0.5413⋅T_0(x) - 0.8991⋅T_1(x) - 0.4238⋅T_2(x)) |
260 | | -``` |
261 | | - |
262 | | -Visual example: |
263 | | - |
264 | | -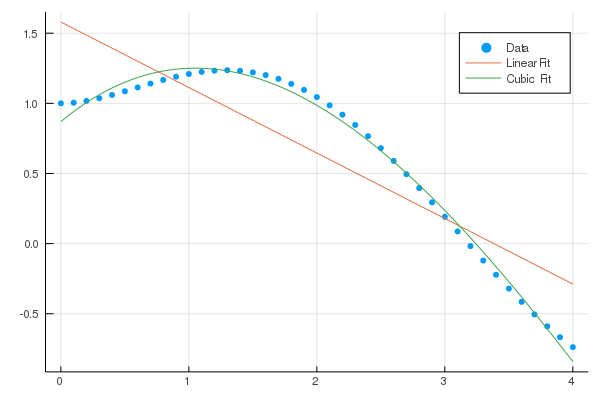 |
265 | | - |
266 | | -### Other methods |
267 | | - |
268 | | -Polynomial objects also have other methods: |
269 | | - |
270 | | -* For standard basis polynomials, 0-based indexing is used to extract |
271 | | - the coefficients of `[a0, a1, a2, ...]`; for mutable polynomials, |
272 | | - coefficients may be changed using indexing notation. |
273 | | - |
274 | | -* `coeffs`: returns the coefficients |
275 | | - |
276 | | -* `degree`: returns the polynomial degree, `length` is number of stored coefficients |
277 | | - |
278 | | -* `variable`: returns the polynomial symbol as a polynomial in the underlying type |
279 | | - |
280 | | -* `LinearAlgebra.norm`: find the `p`-norm of a polynomial |
281 | | - |
282 | | -* `conj`: finds the conjugate of a polynomial over a complex field |
283 | | - |
284 | | -* `truncate`: set to 0 all small terms in a polynomial; |
285 | | - |
286 | | -* `chop` chops off any small leading values that may arise due to floating point operations. |
287 | | - |
288 | | -* `gcd`: greatest common divisor of two polynomials. |
289 | | - |
290 | | -* `Pade`: Return the |
291 | | - [Padé approximant](https://en.wikipedia.org/wiki/Pad%C3%A9_approximant) of order `m/n` for a polynomial as a `Pade` object. |
292 | | - |
293 | | - |
294 | | -## Related Packages |
295 | | - |
296 | | -* [StaticUnivariatePolynomials.jl](https://github.com/tkoolen/StaticUnivariatePolynomials.jl) Fixed-size univariate polynomials backed by a Tuple |
297 | | - |
298 | | -* [MultiPoly.jl](https://github.com/daviddelaat/MultiPoly.jl) for sparse multivariate polynomials |
299 | | - |
300 | | -* [DynamicPolynomials.jl](https://github.com/JuliaAlgebra/DynamicPolynomials.jl) Multivariate polynomials implementation of commutative and non-commutative variables |
301 | | - |
302 | | -* [MultivariatePolynomials.jl](https://github.com/JuliaAlgebra/MultivariatePolynomials.jl) for multivariate polynomials and moments of commutative or non-commutative variables |
303 | | - |
304 | | -* [PolynomialRings.jl](https://github.com/tkluck/PolynomialRings.jl) A library for arithmetic and algebra with multi-variable polynomials. |
305 | | - |
306 | | -* [AbstractAlgebra.jl](https://github.com/wbhart/AbstractAlgebra.jl), [Nemo.jl](https://github.com/wbhart/Nemo.jl) for generic polynomial rings, matrix spaces, fraction fields, residue rings, power series, [Hecke.jl](https://github.com/thofma/Hecke.jl) for algebraic number theory. |
307 | | - |
308 | | -* [LaurentPolynomials.jl](https://github.com/jmichel7/LaurentPolynomials.jl) A package for Laurent polynomials. |
309 | | - |
310 | | -* [CommutativeAlgebra.jl](https://github.com/KlausC/CommutativeRings.jl) the start of a computer algebra system specialized to discrete calculations with support for polynomials. |
311 | | - |
312 | | -* [PolynomialRoots.jl](https://github.com/giordano/PolynomialRoots.jl) for a fast complex polynomial root finder. For larger degree problems, also [FastPolynomialRoots](https://github.com/andreasnoack/FastPolynomialRoots.jl) and [AMRVW](https://github.com/jverzani/AMRVW.jl). For real roots only [RealPolynomialRoots](https://github.com/jverzani/RealPolynomialRoots.jl). |
313 | | - |
314 | | - |
315 | | -* [SpecialPolynomials.jl](https://github.com/jverzani/SpecialPolynomials.jl) A package providing various polynomial types beyond the standard basis polynomials in `Polynomials.jl`. Includes interpolating polynomials, Bernstein polynomials, and classical orthogonal polynomials. |
316 | | - |
317 | | -* [ClassicalOrthogonalPolynomials.jl](https://github.com/JuliaApproximation/ClassicalOrthogonalPolynomials.jl) A Julia package for classical orthogonal polynomials and expansions. Includes `chebyshevt`, `chebyshevu`, `legendrep`, `jacobip`, `ultrasphericalc`, `hermiteh`, and `laguerrel`. The same repository includes `FastGaussQuadrature.jl`, `FastTransforms.jl`, and the `ApproxFun` packages. |
318 | | - |
319 | | - |
320 | | -## Legacy code |
321 | | - |
322 | | -As of v0.7, the internals of this package were greatly generalized and new types and method names were introduced. For compatibility purposes, legacy code can be run after issuing `using Polynomials.PolyCompat`. |
323 | | - |
324 | | -## Contributing |
325 | | - |
326 | | -If you are interested in contributing, feel free to open an issue or pull request to get started. |
0 commit comments