Connections between Support Vector Machines, Wasserstein distance and gradient-penalty GANs #17
Description
0. 論文情報・リンク
- 論文リンク：https://arxiv.org/abs/1910.06922
- 公開日時：2019/10/15
- 被引用数（記事作成時点）：- 件
- 実装コード：https://github.com/AlexiaJM/MaximumMarginGANs
- Publication :
1. どんなもの？
- SVMsやGANsにおける理論を抽象化し，同じ枠組みで説明できることを示した
- WGANよりも優れたGradient Penaltyの提案
- SVMsはGANsのtrivial case
2. 先行研究と比べてどこがすごいの？
-
SVMsは1995に提案され，マージン最大化に基づく分類器として有名である．
SVMsをカーネルトリックによって非線形空間へと拡張した例などはあるものの，つい最近までSVMsを非線形分類器(e.g. ニューラルネットワーク)として一般化した研究はなかった．
そこで著者らは，SVMsを マージン最大化分類器（Maximum-Margin Classifiers） として一般化することでSVMs, GANs および Wasserstein’s distanceを同じ枠組みで捉えなおし，それらの理論的な接続を試みた．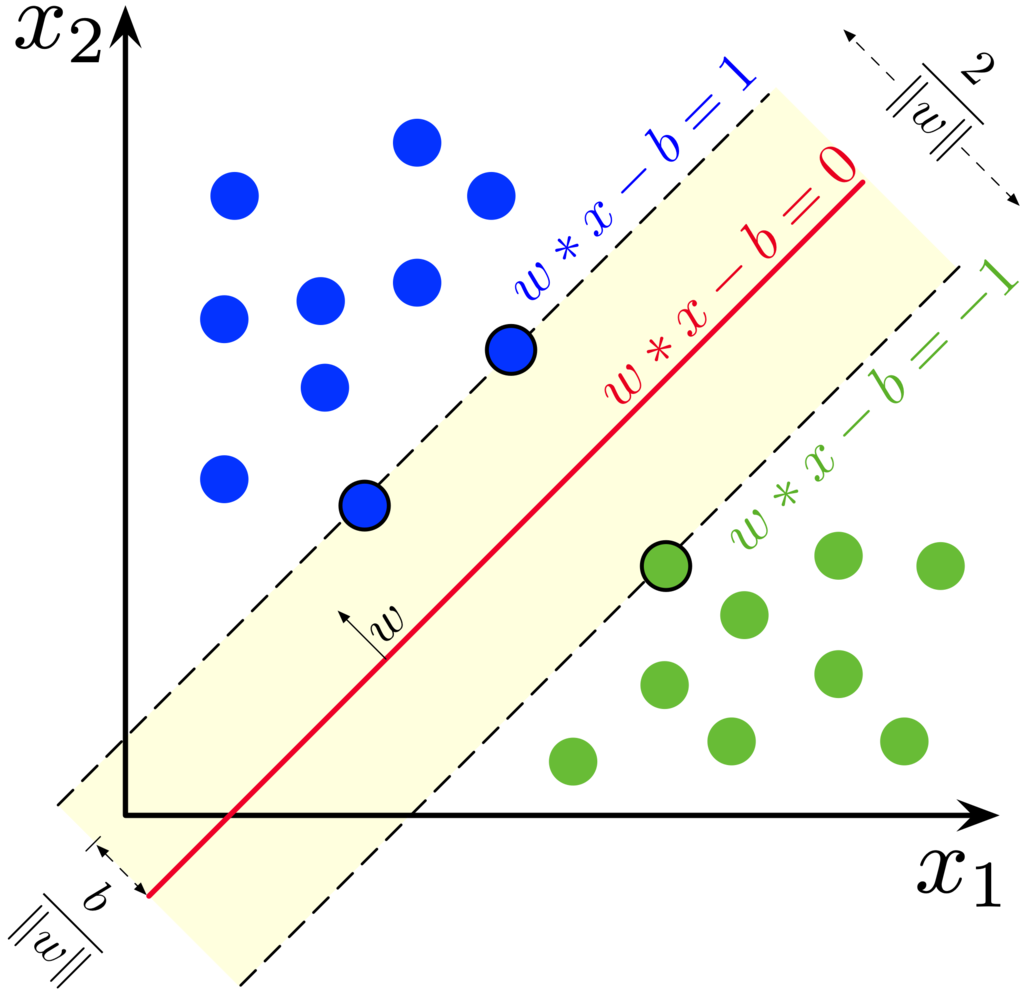
マージンとは分類器のdecision boundaryとそれに最も近い点とのLp距離であり，それが最大となるようなdecision boundaryを選ぶことがマージン最大化である，という認識が世間一般的であるが実際には少し違う．
というのもマージンには「データ点と決定境界の最小距離」という見方があり(これをmargin of a sampleという)，先ほどの「決定境界に最も近い点との距離」という定義(margin of a dataset)ではSVMsの文脈で使用される functional marginおよび geometric margin
が"マージン"とみなされない．
本論文ではこのような背景を鑑みて「データ点と決定境界の最小距離」をマージンの定義として採用する． -
GANsはおそらく最も成功した生成モデルであり，Generatorによる出力と実データを見分けるDiscriminator，およびDiscriminatorを騙すような本物に近い出力をするGeneratorの２つのニューラルネットワークからなる．
GANsの学習は一般的に不安定であるが，Gradient PenaltyによってDiscriminatorの勾配に制限を加えることがいくらかの安定化に寄与すること[1][2]が知られている．
このGANsにおけるGradient Penaltyの利用もMMCs(Maximum-Margin Classifiers)の特殊な形として解釈できる．
3. 技術や手法の"キモ"はどこにある？
-
Penalized GANs
GANsの目的はrealデータとGeneratorが生成するfakeデータの確率分布を近づけることにある．
このとき２つの確率分布の距離を測る指標としてIPMs ( Integral probability metrics) を用いるGANsが存在し大変重要である (ちなみに通常のGANsはIPMsではなくJS-divergenceを用いる)．
IPMsは以下の式
ここでPは真のデータの分布，Qはfakeデータの分布，Fは実数関数の集合，Cは評価関数を表す．
IPMsに基づいた手法としてWGANやWGAN-GPがある．WGANはGANの学習におけるモード崩壊（Generatorの出力が一様になること）を抑制できることで知られる．
また，WGANは２つの確率分布の距離指標に１次のWasserstein距離を用い，このときIPMは1-リプシッツ関数によるものに限られる．
ここで1-リプシッツ関数はを満たす．
WGANは学習の更新の度に評価関数Cの重みWをクリップし，Wのパラメータ空間を小さくとることでリプシッツ連続性を保とう（Cの傾きをboundしよう）とする．これは簡単かつ強力な方法ではあるが，後述するようにいくつかの理論的欠陥の原因になる．
Improved-WGANにおいては，最適な評価関数C*(x)は全域で微分可能かつ，最適な(x_1,x_2)の同時確率分布の場合はであるため，
であることが示された．
実際は，最適な同時確率分布からのサンプリングが不可能であることと，C*の微分可能性が保証されないため，この方法は近似に留まる．
評価関数Cのリプシッツ連続性のための勾配制約の他にも，gradient norm penaltyを利用した学習をするGANはHingeGAN, RpGANs, RaGANsなど多く存在する．
-
SVMの一般化
以下の話は簡単のために厳密性を省く(詳細は論文を参照)．
SVMsにおけるマージンは分類機の線形性を仮定すれば(テイラー展開の一次近似を考えれば)の形に書ける．より一般的には関数F, gによってマージン最大化を
のように書くこともできる．
SVMsは典型的にはgとしてを選びこれは
の制約に対応する．
しかし，zは確率変数であり全てにおいて1であるという制限は厳しいという見方もある．そのような場合のように緩めた条件を選択できる．
上で見たようにSVMを厳密に数式化するには，線形性を仮定しなければならなかったが決定境界にはサンプルが存在しないため勾配が最小化できない一方でマージンは最大化しなければならないというジレンマがある．ただ，上のマージン最大化の式で見るように yf(x)の最大化と，gradient penaltyの最小化に分けて考えれば近似は不要になる．
決定領域に近いサンプルにペナルティを加えることにすれば、決定領域に近いサンプルを探しマージンを広げるといった操作は不要になる。しかしながら、決定領域付近のサンプリングは依然として課題である。単純な解決として、クラス1とクラス2のサンプルの線形補間を取ることとすれば、のようになる。これはWGANにおける補間と同じ！
-
Connections to GANs
SVMsの一般化によって、gradient penaltyと目的関数の和の期待値最大化問題が得られた。
罰則ありのGANsとSVMsの接続を明確にしたい。
いま、g(z)として(z-1)^2を選べば、目的関数F(z)=zのときがWGAN-GP, log(sigmoid(z))がStandard GAN, -(1-z)^2がLSGANおよび -max(0, 1-z)がHingeGANにそれぞれ対応する。
すなわち罰則ありGANsはすべてL2マージン最大化とみなすことができる。
-
勾配正則化とリプシッツ関数の等価性
WGANにおけるWasserstein距離の評価が、評価関数の勾配制限による方法では近似に留まっていたことは既に述べた。
勾配のLpノルムをのようにとることで、関数fのＫ−リプシッツ性が保証される。このとき逆も成り立つ。すなわち，である。
まとめるとWasserstein距離はの制約よってより効率よく近似が可能である。
-
L2マージンよりベターなマージンは存在するか？
Lpノルムはpが大きくなるほど外れ値に敏感であり、L1ノルムが多くのロバストな誤差関数に用いられている。
L∞に基づく勾配正則化はL1ノルムでのマージン最大化に相当し、L2勾配正則化（このときpも2になる)よりもロバスト性を高めることができると推察される。
4. どうやって有効だと検証した？
罰則ありGANsはL2マージンを考えていたが前述の議論より，L1マージンに対応したL∞勾配正則化を選んだ方がパフォーマンスが良いはずである．
また，Generatorの勾配消失を軽減するため(論文参照)，ペナルティのかけ方はよりも
が適すと考えられる．
このことを確かめるため，検証実験をデータセットとしてCIFAR-10を選び行った．
パラメータは勾配関数gとノルムのかけ方pである．
すなわち，にはLeast Squares (g(z)=(z-1)^2),
にはHinge Loss (g(z)=max(0,z-1))を対応させて選び，またpは1, 2, ∞のどれかである．
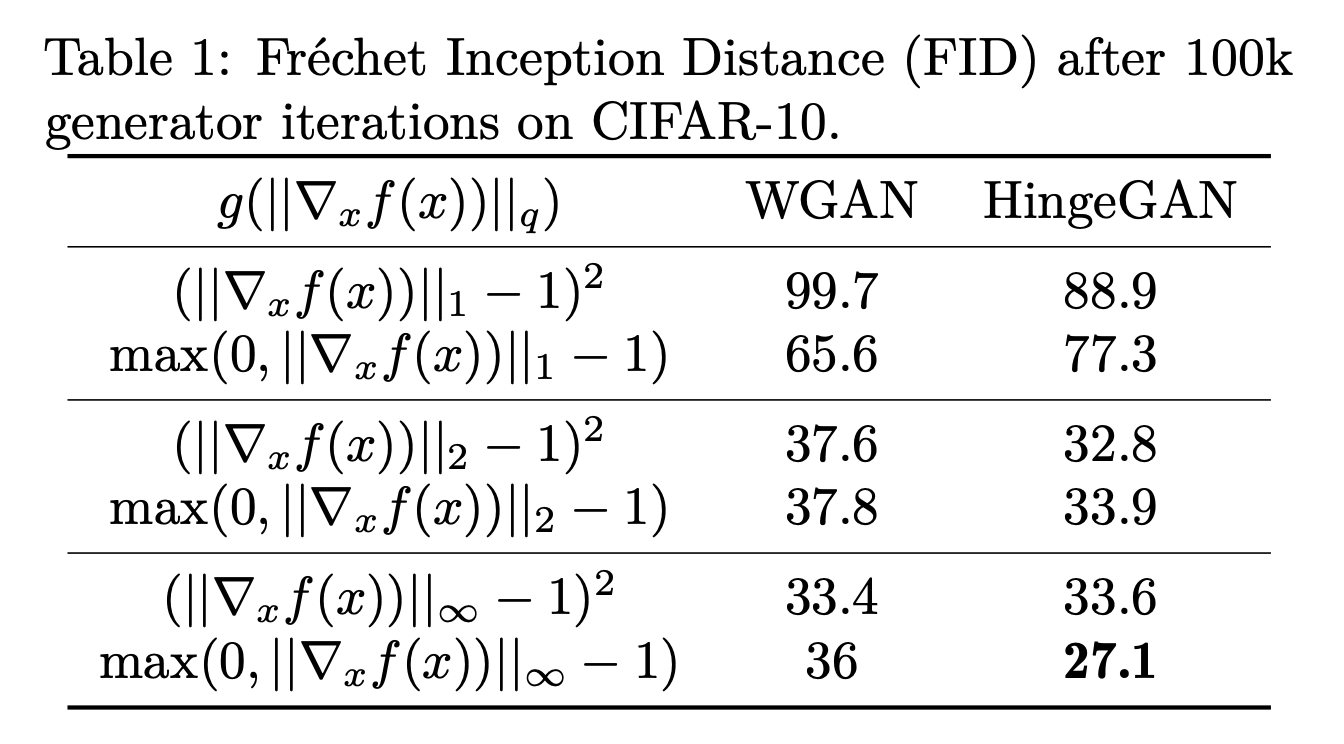
結果は理論的帰結から得られたものと同じく、L∞勾配正則化とHinge Lossの組み合わせで最も低いFIDスコアになった。
5. 議論はあるか？
理論的な論文らしく数式を使って詳細な議論をしてくれているし，説明もわかりやすい．加えて実データによる実験もなされていて説得力がある．
ただ，実験についてはモード崩壊が起こりにくく良い学習方法であること≒FIDスコアが低いという関係はどのくらい成り立つのかという疑問はある．
また，決定境界付近の勾配を得るために2クラスのサンプルの線形補間を考えているが，これはもっと良い方法がありそう．
勾配ペナルティの与え方はHinge Loss以外が適す場合も考えられる．しかしどんな例があるかは分からないし，理論的にこれが良さそうというのも現時点では検証できない．
いずれにせよ，罰則ありGANs（今回でMMCsとして拡張された）については，まだ数式で詰めれる部分はありそう．
6. 次に読むべき論文はあるか？
xxx
7. 参考文献
著者本人によるブログ
[1] Wasserstein GAN (https://arxiv.org/abs/1701.07875)
[2] Improved Training of Wasserstein GANs (https://arxiv.org/abs/1704.00028)