Full-Gradient Representation for Neural Network Visualization

[Kaniikura]

一言でいうと

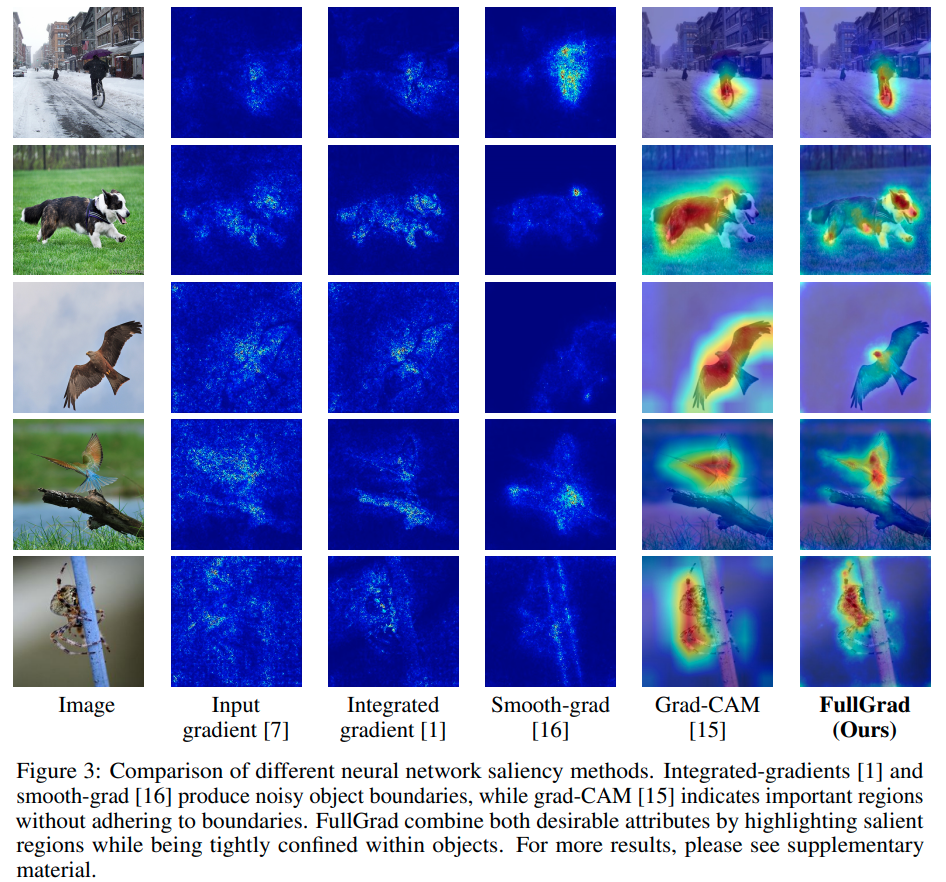
Grad-CAMに代表される、モデルの入力に対する注意箇所の可視化(saliency map)に関する研究。
saliency mapにはcompletenessとweak dependenceの２つが要求されるが、同時に解決することは困難であった。
提案手法であるFullGradは初めてこの問題に取り組み、従来手法と比べ改善を示した。

論文リンク

https://arxiv.org/abs/1905.00780

著者/所属機関

Suraj Srinivas, François Fleuret

• Idiap Research Institute & EPFL

投稿日付(yyyy/MM/dd)

2019/12/03

概要

• 顕著性マップ(Saliency Map)
• 画像の中で人が見たときに特に注目するであろう箇所を、色付けで可視化したもの。
  
  特に深層学習の文脈では、画像クラス分類モデルの判断根拠を示し、ネットワークの解釈妥当性を検証するために登場することが多い。

• completeness と weak dependence
• 顕著性マップには直観的に要求される事項が２つある。（しかし、既存のモデルではその２つの要求を同時に解決したものは存在しない！）
  
  まず１つ目の性質は、「もし入力の一部がその値を変えていったとき、モデルの出力に大きな影響を及ぼすならばその箇所は重要であると見なされる」といった事実から導かれ、これをlocal attributionという。
  
  ２つ目は「顕著性マップはモデルの出力を完全に説明する性質をもつべきであり、この視点ではモデルの数値的な出力は、入力の各特徴量に分配され得ると考えられる（出力は入力の各特徴量重要度の足し合わせと言い換えてもいい）」という知見から得られたglobal attributionという考えである。
  
  （注釈：出力の数値を入力に再分配するということは、CNNでは逆伝搬でdeconvを作用させる的なことに相当し、入力の大域的な特徴の重要度を捉えることが可能なためglobalと言っているのだと思う。）
  
  そもそも顕著性マップにおいて難しいのはピクセル単位では捉えきれない重要度が存在することである。 例えば、自転車の画像においてドット抜けがあったところで、さしたる問題にはならないがフレームやタイヤがまるごと抜け落ちたときはおそらくモデルの解釈性に問題をきたす。これを、ピクセルの集合としての重要性という。
  
  saliency mapをつくるとき、入力自体を考えるとピクセル単位になってしまうが、中間層のニューロンに注目すると大域的な入力の特徴量について考慮できる。 本研究ではlocal attributionとglobal attributionの双方を扱った full-gradientsという仕組みを導入した。


• 本研究の貢献は大きく分けて３つ
  1. 直観的な知見としてのlocal attributionとglobal attributionを、それぞれweak dependenceとcompletenessとして定式化した。そして数式的な帰結として、saliency mapではこれら２つを同時に解決することはできないことを示した。
  2. saliency mapsよりも表現力があり、前述した２つの要求を同時に満たすことのできるfull-gradientsを導入した。また、CNNにおいてfull-gradientsを近似してsaliency mapをつくるための手法としてFullGradを提案した。
  3. pixel perturbation とremove-and-retrainと呼ばれる評価法を利用して、FullGradが既存のsaliency map手法よりも優れていることを定量的に示した。

手法

• Local vs. Global Attribution
• local attributionとglobal attributionを同時に満足するようなsaliency mapが存在しないことを示す。
  ニューラルネットワークf : R^D -> R with inputs x ∈ R^D（D次元入力に対し１次元の出力を与える）を考える。
  ここで、モデル fと入力 xについてのsaliency mapはS(x) = σ(f, x)と表せる。
  線形モデルを仮定するとf(x) = w^T x + bであり、wそのものがsaliency mapになるがこれは入力 xに依存しない。
  そこで、入力が属す集合によってパラメータが変わるような関数を線形モデルの寄せ集めで表現することを考える。
  
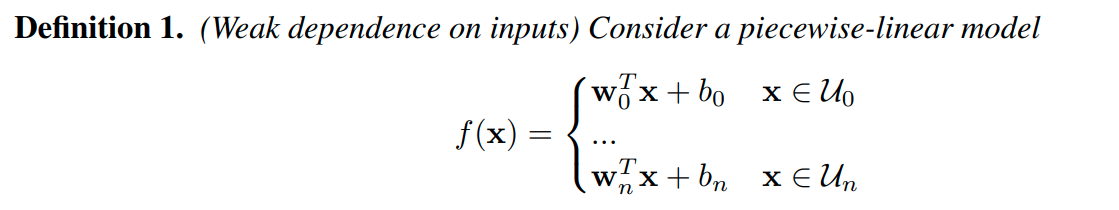
  これはlocal importanceの線形モデルにおける一般化表現になっている。
  （入力 x自体に Sは依存しないが、 x がどの集合 Uiに属すかには依存するといった間接的な依存が生じている。）
  
• 次にcompletenessの数学的な定義を確認してみる。
  
  ざっくり言えば、S(x)はモデル fの計算を完全に捉えた表現になっていなければならないこと、すなわちsaliency map S(x) と入力 xによって fが復元されることを保証するものがcompleteness(完全性)である。
  
• 上記の数学的な表現を駆使すると、weak dependenceとcompletenessを同時に満たすsaliency mapは存在しないことを示せる（らしい）。
  実際に既存手法であるintegrated gradients, deep Taylor decomposition, DeepLIFTはcompletenessのみを満たすものとして存在している。
  
  そもそもsaliency mapは性能が非常に限定されており、線形モデルのweightとbiasを同時に反映させることすらできない。そのため、このように２つの要求を同時に満たすことができないジレンマを抱えている。
  逆に言うと、saliency mapにおいてbiasが無視される問題を解決できればこのジレンマを解決できるのではないかという観点が生じ、これがニューラルネットワークのbiasを考慮したfull-gradientsという仕組みに繋がる。

• Full-Gradient Representation
• 例として、活性化関数にReLUを含んだニューラルネットワークをみてみると、
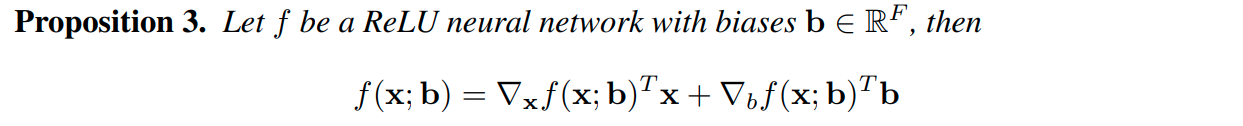
  のような関係式が得られる。
  ここでバイアスbには陽に表されるexplicit biasと陰に表されるimplicit bias（e.g. Batchnormの移動平均）の２種類が存在することに留意されたい。しばしば、implicit biasの方が量的に大きく、ネットワークの中ではexplicit biasよりも重要な存在になるケースが多い。
  
• さて、non-ReLUな活性化関数を含むネットワークについては微分形でimplicit biasが現れないため、上で見た式の拡張を考える必要がある。
  y = σ(x) の x周りの１次近似をすると、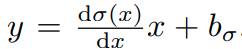 という式が得られる。b_σはimplicit biasであり微分形では現れない(もちろんReLUではb_σ = 0)。すなわちReLUで得られた関係式の bに b_σを加えれば一般的な非線形関数への表現が得られることになる。
  input-gradients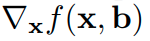と、bias-gradients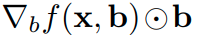を組み合わせたものが full-gradientsになる。
  
• 以下にそれぞれの可視化を示す。
  
  

• Properties of Full-Gradients
• 長くなってしまうので、本文では解説しない。
  （Full-Gradientsの性質について既存手法と比較しながら述べられていて、bias-gradientsがなぜ重要なのか、どのように機能するのかについても例を挙げながら説明されている。興味がある場合は論文を参照のこと。）
  

• FullGrad: Full-Gradient Saliency Maps for Convolutional Nets
• bias-gradientsの可視化は容易で、理由は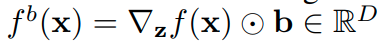は入力 xと同じD次元になるため。
  さて、full-gradientsをもとにした関数 fと入力 xに対するsaliency map(FullGradと呼称 )は以下のようになる。
  
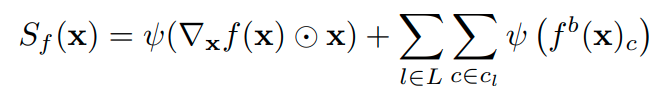
  ここで、 ψ(·)はアップサンプリングやリスケールなどを含んだ後処理である。式を見てわかるようにbias-gradientsはチャンネルごとに総和を取ったものからさらに層ごとに足し合わせることでマッピングしている。なお、CNNにおける全結合層は無視されconvolution層のみが上式に含まれる。
  
• 注意したいのは、FullGradはfull-gradientsの近似表現になっていることである。
  full-gradientsは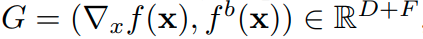というようにF+D次元になっており、FullGradはサイズの調整を行ってわざわざ入力画像と同じ次元となるような表現を得たものに過ぎない。
  したがってcompleteness と weak dependenceが同時に達成されることはない。ただ、上式のsaliency mapの作り方を変える( ⦿ xの除去や ψ(·)の調整)ことでどちらか片方の性質を強めることができ、筆者らの実験では上式の表現が最もシャープなmapを作れたそうである。

結果

評価方法は大きく分けて２つ。

1. Imagenet 2012 datasetでpixel perturbation
2. CIFAR100 datasetでremove and retrain procedure

Pixel perturbation

saliency mapから最も強度の強い kピクセルを取り除く手法。

この手法によって、良いsaliency mapであればネットワークの出力に大きく影響を及ぼすピクセルを取り除く（黒で置き換える）ことになると考えられる。しかし筆者らは、重要なピクセルを黒で置き換える方法では正確にsaliency mapの性能を測れない（実際にランダムにピクセルを置き換えたときのほうがモデルの性能には悪影響であるという結果になった）とし、saliency mapの強度が小さい k個を取り除くことを提案した。

VGG-16をモデルに採用し、gradCAM, input-gradients, smooth-gradと integrated gradientsについて比較した結果が下図(a)である。

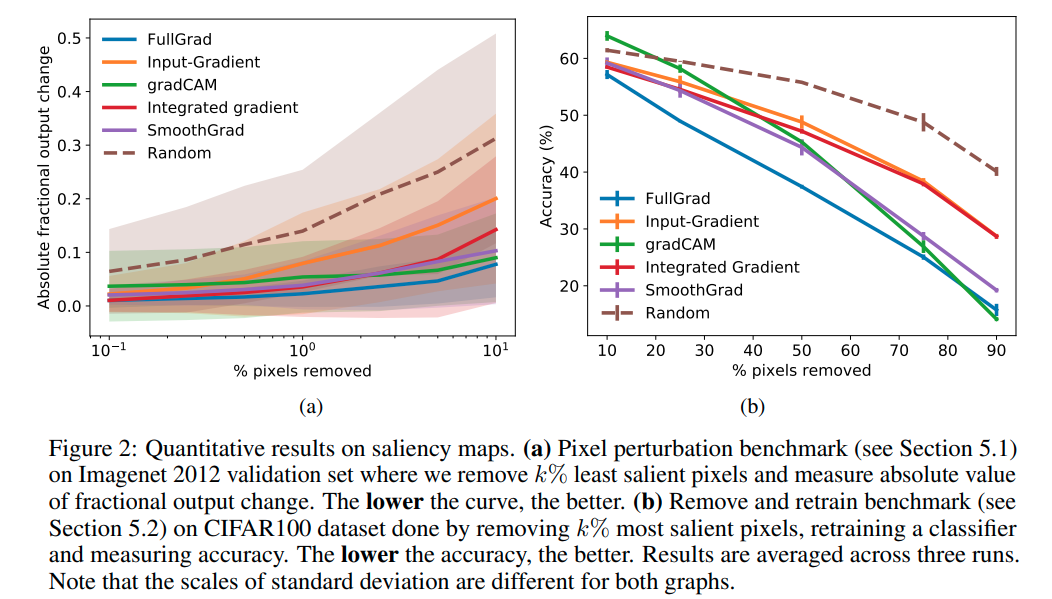
RemOve And Retrain (ROAR)

saliency mapのtop-kピクセルを取り除いた画像データセットをつくり、モデルを訓練し直す手法。
もし重要度の高いピクセルを捉えることに成功していたら、より訓練したモデルの性能が悪くなるはずであるという仮定にもとづく（ただ、重要なピクセルの位置が情報として残ってしまうなどの欠点のある手法ではある）。

Pixel perturbationでは重要度の低いピクセルに注目していたので、重要度の高いピクセルに焦点をあてた本手法と合わせることで両面的に評価することができる。

VGG-16をモデルに採用し、データセットはCIFAR-100でgradCAM, input-gradients, smooth grad squaredと integrated gradientsについて比較した結果が上図(b)である。

Visual Inspection

コメント