Easily plot and compare multiple marginal posteriors

[hectormz]

I wanted a way to efficiently compare multiple marginal posteriors in PyMC3/ArviZ like in Figure 9.10 from Kruschke's book:

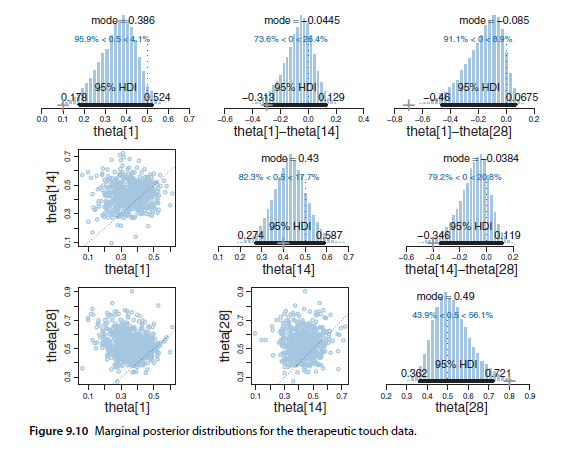
This is especially the case when using vectorized parameters in a model, and I'd like to compare many/all of them. If I have two, creating a pm.Deterministic difference isn't bad.

I searched PyMC3/ArviZ documentation and examples, and didn't seem to find anything that fit this need. Forest plots give similar answers, but comparing HPDs of two parameters is not the same as looking at the HPD of their difference.

I created a function to plot the difference in marginal posteriors.

from matplotlib import pyplot as plt
import numpy as np
import pymc3 as pm
import arviz as az


def compare_posterior(
    trace,
    var_name,
    triangle="lower",
    identity=True,
    figsize=None,
    textsize=None,
    credible_interval=0.94,
    round_to=3,
    point_estimate="mean",
    rope=None,
    ref_val=None,
    kind='kde',
    bw=4.5,
    bins=None
):
    triangle_options = ("lower", "upper", "both")
    assert (
        triangle in triangle_options
    ), f"triangle argument must be 'lower', 'upper' or 'both'."
    
    num_param = trace[var_name].shape[1]
    if figsize is None:
        figsize=(num_param * 2.5, num_param * 2.5)
        
    fig, axes = plt.subplots(num_param, num_param, figsize=figsize)
    for i in range(num_param):
        for j in range(num_param):
            ax = axes[i, j]
            if triangle is "lower" and i < j:
                ax.axis("off")
                continue
            elif triangle is "upper" and i > j:
                ax.axis("off")
                continue

            if i is not j:
                az.plot_posterior(
                    trace[var_name][:, i] - trace[var_name][:, j],
                    ref_val=ref_val,
                    ax=ax,
                    textsize=textsize,
                    credible_interval=credible_interval,
                    round_to=round_to,
                    point_estimate=point_estimate,
                    rope=rope,
                    kind=kind,
                    bw=bw,
                    bins=bins,
                )
                ax.set_xlabel(f"{var_name}_{i} - {var_name}_{j}")
            else:
                if identity:
                    az.plot_posterior(
                        trace[var_name][:, i],
                        ax=ax,
                        textsize=textsize,
                        credible_interval=credible_interval,
                        round_to=round_to,
                        point_estimate=point_estimate,
                        kind=kind,
                        bw=bw,
                        bins=bins,
                    )
                    ax.set_xlabel(f"{var_name}_{i}")
                else:
                    ax.axis("off")
    plt.tight_layout()
    return axes

# Generate data
N = 1000
W = np.array([0.35, 0.4, 0.25])
MU = np.array([1.8, 2., 2.2])
SIGMA = np.array([0.5, 0.5, 1.])
component = np.random.choice(MU.size, size=N, p=W)
x = np.random.normal(MU[component], SIGMA[component], size=N)

# Build and run model
with pm.Model() as model:
    # define priors
    mu = pm.Uniform('mu', lower=0, upper=10, shape = MU.size)
    sigma = pm.Uniform('sigma', lower=0.001, upper=10, shape=MU.size)
    # likelihood
    likelihood = pm.Normal('likelihood', mu=mu[component], sd=sigma[component], observed=x)
    trace = pm.sample(2000, tune=2000, cores=2, chains=3)

# Plot
compare_posterior(
    trace,
    var_name="mu",
    triangle="lower",
    ref_val=0,
    credible_interval=0.95,
)
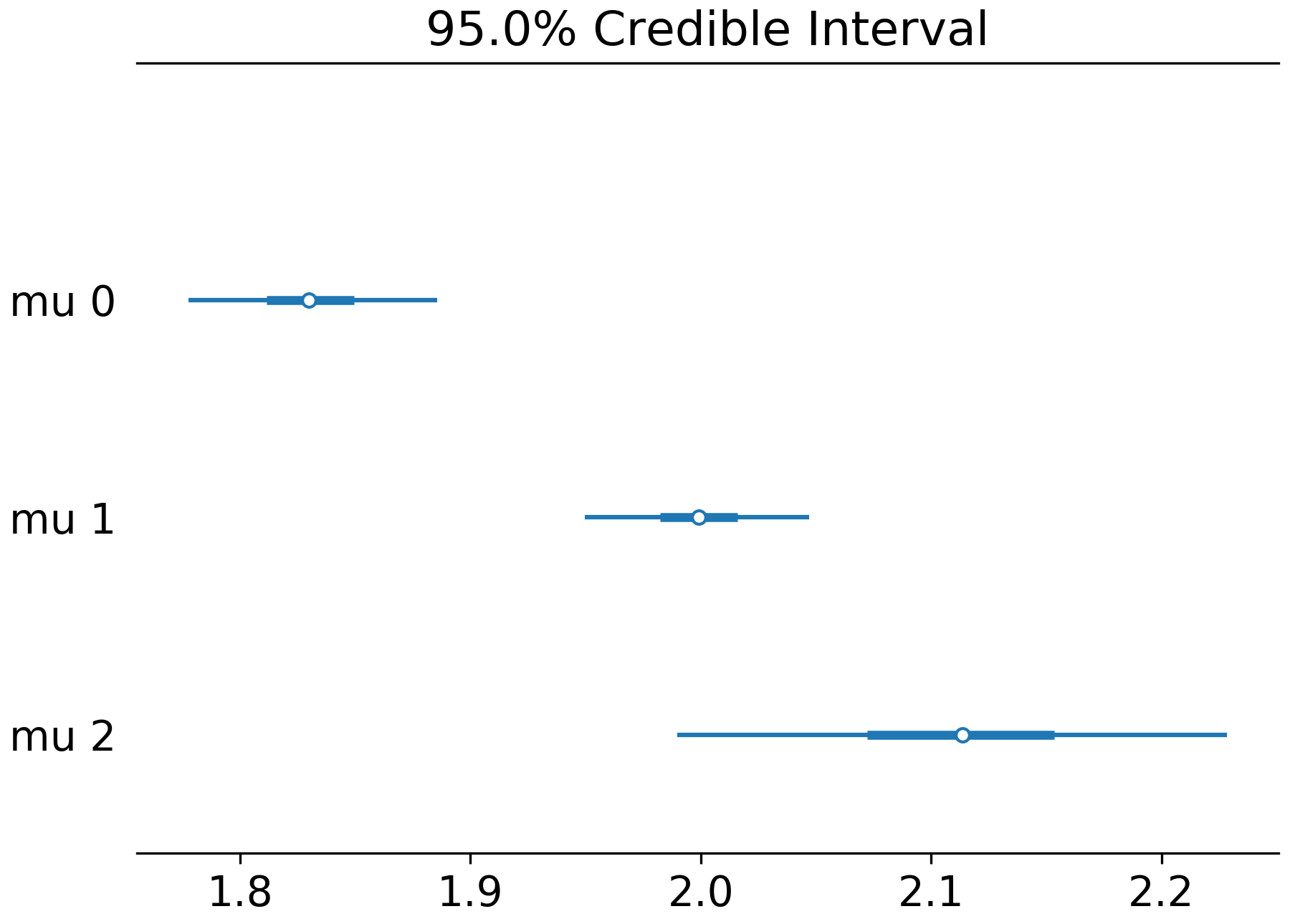
plt.show()

Here's the combined forest plot for the same trace:

I didn't care about recreating the scatter plots, but the function could be modified to faithfully recreate the original figure:

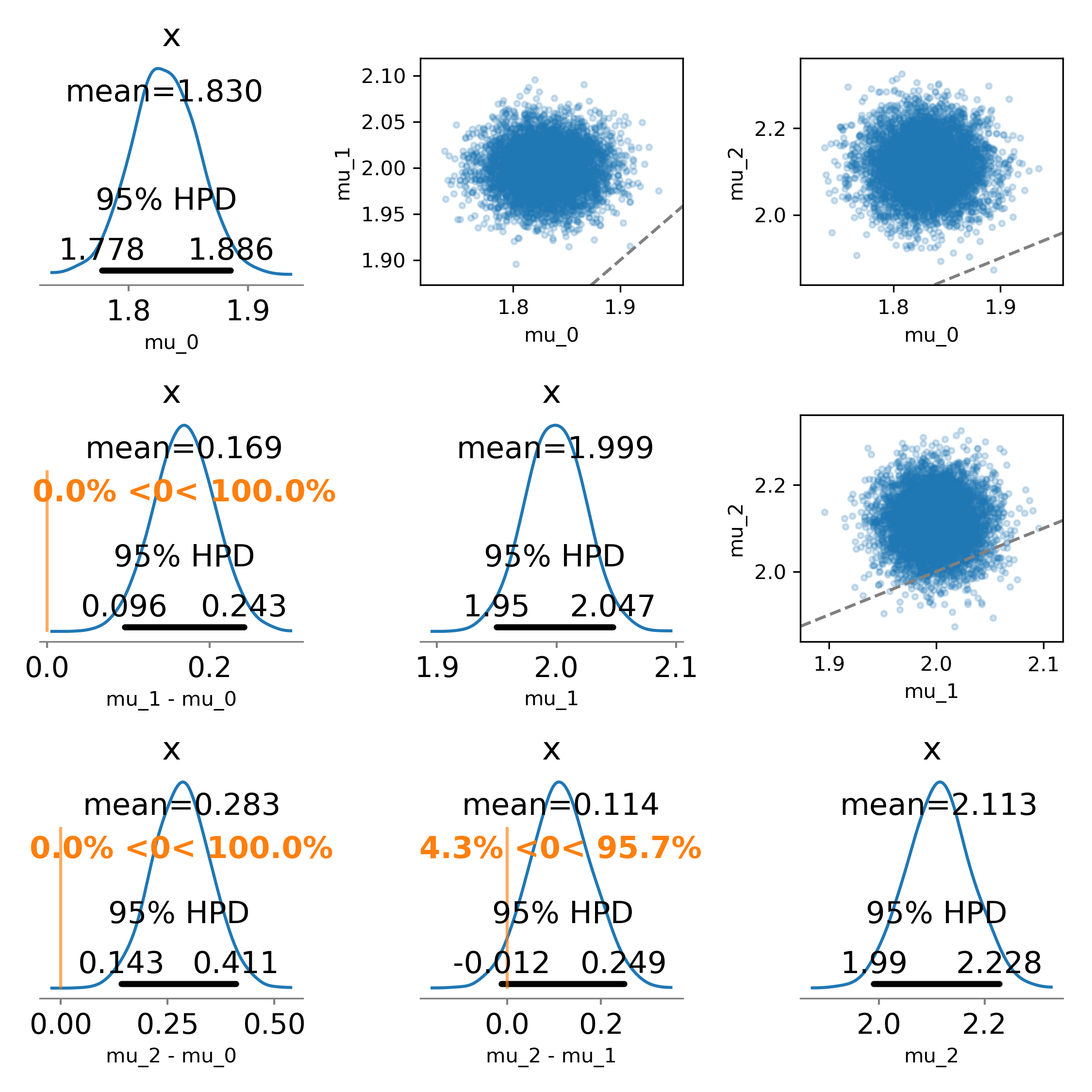
The results (and interpretations) may be different from what you'd get from a forest plot, depending on the data and parameters.

My function assumes that only one parameter would be compared at a time, and assumes that the parameter vector is a reasonable length. It's a little hackish, and assumes a PyMC3 trace for data.

Is this something worth adding to arviZ? Is there any reason that these types of plots are invalid or shouldn't be encouraged? If there's interest, I'd be willing to build this into a PR to add to arviZ (and PyMC3 plotting).

[aloctavodia]

Hi @HectorM14 thanks for this contribution, the plot looks really nice. It will be really great if you send a PR with this new plot. Please use our existing plots as a reference, maybe pair_plot is a good place to check.

[hectormz]

@aloctavodia I'll work on a PR that follows the current format as existing plots. Thanks! I'll check in if I have questions.

[OriolAbril]

I volunteer to help with the PR. In fact this issue has given me the idea of extending plot pair using customizable functions.

There would be 3 input functions, each with its own kwargs:

• lower triangular function
• upper triangular function
• diagonal function

The triangular functions should have as arguments values1, values2, ax, and the diagonal one values1, ax. If one of these functions were None, ax.axis("off") should be called.

The skeleton would be quite similar to plot_pair. Therefore, using plot_posterior as diagonal function and as lower triangular a wrapper on plot posterior similar to this:

def difference_hist(values1,values2,ax,**kwargs):
    return az.plot_posterior(values1-values2,ax=ax,**kwargs)

should generate your first output. Adding plot_kde or a wrapper on plot_pair as upper triangular function should generate your second output. The default could be a plot pair with the marginal distributions on the diagonal, and nothing on the upper triangle which is a quite common plot.

[hectormz]

Hi @OriolAbril , I agree, this could be very clean and simple since it mostly relies on existing plotting functions in arviZ.

In my first draft of my function that I included, I was only interested in plotting kde/histograms, and I wanted to make all the arguments explicit for the user (me), instead of capturing everything as **kwargs and passing them to plot_posterior. Adding another triangle (scatter/kde/hexbin) because if all the passed arguments are explicit, the list grows a bit, OR we're capturing kwargs for the two triangles, and have to separate them before passing them along.

What do you think about that? Should there be many explicit and obvious options for the user, or should they know which arguments to pass?:

def plot_compare_posterior(data, var_name, lower='hist', upper='kde', **kwargs):

As I previously thought about it, (compared to plot_posterior) a user would only want to compare a single var_name, and optionally provided a list of indices if they don't want to compare every item in the vectorized posterior.

What would be an appropriate name for this plot?

[OriolAbril]

About the arguments I would start with:

def plot_pair_extended(
    # arguments needed to mimic plot_pair
    data, var_names=None, coords=None, figsize=None, ax=None, 
    # function arguments
    lower_fun=plot_kde, upper_fun=None, diag_fun=plot_posterior,
    # function kwargs, as the functions are independent, their kwargs should be too
    lower_kwargs=None, upper_kwargs=None, diag_kwargs=None):

The coords will allow to select some of the items in var_names. In addition however, it may be useful to compare different chains instead of all draws.

As for the name, I could not think of anything else other than pair_plot_extended. But I would not worry about it too much about it yet.

[OriolAbril]

I was thinking that changing the arguments of the triangle functions to values, ax like in the diagonal case, with the difference of values being 2D instead of 1D will probably ease the default values and creating (or even better avoid creating) wrappers. For instance, plot_pair itself could be used as lower triangular function default. This would allow more freedom in the kind of pairplot used.

[hectormz]

If I follow you correctly:

• the diagonal will always be default plot_posterior (if shown), and the user can still pass along specific kwargs
• one triangle will always be default plot_posterior (if shown), and the user can still pass along specific kwargs
• the other triangle will always be default plot_pair (if shown), and the user can still pass along specific kwargs

I think that is along the lines of what I was previously thinking. With that reasoning though, if I only wanted one of the triangles, the type of plot I want, and where I want it, may differ from someone else. But I think we could include some default boolean argument that handles that desire.

Referring to the triangle options by their position (upper/lower) is intuitive, but we could also refer to them as the 1D or 2D comparisons as you mentioned.

I did most of my work only in PyMC3 until recently, but I'm now seeing how great InferenceData and coords in arviZ are for these plots

[hectormz]

Will coords allow the user to select particular (or all) chains to compare, or that is another matter that you were bringing up?

[OriolAbril]

I had in mind to use functions as parameters, therefore, the diagonal and both triangular plotting functions can be any function defined by the user. That is why in the definition of plot_pair_extended nor plot_kde nor plot_posterior are strings. Therefore, a typical use case would be:

import arviz as az
# define simple function to plot the difference
def difference_hist(values1, values2, ax):
    ax = az.plot_posterior(values1-values2, ax=ax, kind='hist')
    return ax

data = az.load_arviz_data('centered_eight')
# call plot_pair extended overriding the default lower triangular function
az.plot_pair_extended(data, var_names=["mu"], lower_fun=difference_hist)

There are no quotes around difference_hist in order to pass the function to plot_pair_extended Hence, calling lower_fun(x, y, ax) inside plot_pair_extended will be equivalent to calling difference_hist(x, y, ax) in the main program.

In order to leave one of the triangles or the diagonal empty, None could be passed as function (like the default for upper_fun) to avoid an extra boolean function.

The coords argument will allow to use only the subset defined there to do the plots, but not to compare between chains (i.e. creating a plot pair comparing the first and second chain of the same dimension of the same variable). This is going one step further. Moreover, plot_pair does not allow that, therefore, the skeleton will have to be modified in order to include this chain comparison functionality.

[hectormz]

Hi @OriolAbril , the functions as parameters makes sense. I was thinking of creating the the function that subtracts and plots the two posteriors in a way that we still pass it data, var_names, coords, and it figures out what to plot, so that it can be interchangeable with all the other types of plots that might be used throughout the grid.

Following your advice, here is a rough attempt. It's missing a lot of the bells and whistles from pair_plot etc, but I think it gets the point across. In addition to pair_plot_extended and plot_dist_diff, I made a helper function for both gen_var_dims_list, that gathers the valid pairs between var_names and coords that will be plotted:

import matplotlib.pyplot as plt
from ..data import convert_to_dataset
from ..plots.plot_utils import purge_duplicates, get_coords, _scale_fig_size
from .posteriorplot import plot_posterior
from .pairplot import plot_pair
from itertools import product


def gen_var_dims_list(data, var_names, coords):
    """Generate list of valid var_names and coords pairings
    """

    # If value for key in coords is string and not list of string(s),
    # parameter_list does not build properly
    for j in coords:
        if isinstance(coords[j], str):
            coords[j] = [coords[j]]

    posterior_data = convert_to_dataset(data, group="posterior")
    posterior_data = get_coords(posterior_data, coords)
    skip_dims = set()
    skip_dims = skip_dims.union({"chain", "draw"})
    var_dims_list = []
    for var_name in var_names:
        if var_name in posterior_data:
            new_dims = [dim for dim in posterior_data[var_name].dims if dim not in skip_dims]
            vals = [purge_duplicates(posterior_data[var_name][dim].values) for dim in new_dims]
            dims = [{k: v for k, v in zip(new_dims, prod)} for prod in product(*vals)]
            var_dims = [[var_name, d] for d in dims]

            var_dims_list += var_dims

    return var_dims_list


def plot_dist_diff(data, var_names, coords, textsize=None, figsize=None, ax=None, **kwargs):
    var_dims_list = gen_var_dims_list(data, var_names, coords)

    assert len(var_dims_list) == 2, "Too many parameters provided"

    (figsize, ax_labelsize, _, xt_labelsize, _, _) = _scale_fig_size(
        figsize, textsize, 1, 1
    )

    if ax is None:
        fig, ax = plt.subplots(figsize=figsize, constrained_layout=True)

    var_name_0 = var_dims_list[0][0]
    var_name_1 = var_dims_list[1][0]
    coord_0 = var_dims_list[0][1]
    coord_1 = var_dims_list[1][1]

    if len(coord_0) == 1:
        coord_0_suff = "_" + list(coord_0.values())[0]
    else:
        coord_0_suff = ""
    if len(coord_1) == 1:
        coord_1_suff = "_" + list(coord_1.values())[0]
    else:
        coord_1_suff = ""

    diff_DataArray = data.posterior[var_name_0].sel(coord_0) - data.posterior[
        var_name_1
    ].sel(coord_1)

    diff_var_name = f"{var_name_0}{coord_0_suff} - {var_name_1}{coord_1_suff}"

    data.posterior[diff_var_name] = diff_DataArray
    plot_posterior(data, var_names=[diff_var_name], ax=ax, **kwargs)


def pair_plot_extended(data, var_names, coords=None, lower_fun=plot_pair, upper_fun=None, diag_fun=plot_posterior,
                       lower_kwargs=None, upper_kwargs=None, diag_kwargs=None):
    if coords is None:
        coords = {}

    if lower_kwargs is None:
        lower_kwargs = {}

    if upper_kwargs is None:
        upper_kwargs = {}

    if diag_kwargs is None:
        diag_kwargs = {}

    var_dims_list = gen_var_dims_list(data, var_names, coords)
    fig, axes = plt.subplots(len(var_dims_list), len(var_dims_list), figsize=(10, 10))

    for i in range(len(var_dims_list)):
        for j in range(len(var_dims_list)):
            sub_var_name = purge_duplicates([var_dims_list[i][0], var_dims_list[j][0]])
            if len(var_dims_list[i][1]) > 0 and len(var_dims_list[j][1]) > 0:
                if list(var_dims_list[i][1].keys())[0] in var_dims_list[j][1]:
                    dict1 = var_dims_list[i][1]
                    dict2 = var_dims_list[j][1]
                    sub_coords = {
                        i: purge_duplicates(list(j))
                        for i in dict1.keys()
                        for j in zip(dict1.values(), dict2.values())
                    }
                else:
                    sub_coords = {**var_dims_list[i][1], **var_dims_list[j][1]}
            else:
                sub_coords = {**var_dims_list[i][1], **var_dims_list[j][1]}

            ax = axes[j, i]
            if i < j:
                if lower_fun is not None:
                    lower_fun(data, var_names=sub_var_name, coords=sub_coords, ax=ax, **lower_kwargs)
                else:
                    ax.axis("off")
            elif i > j:
                if upper_fun is not None:
                    upper_fun(data, var_names=sub_var_name, coords=sub_coords, ax=ax, **upper_kwargs)
                else:
                    ax.axis("off")
            elif i == j:
                if diag_fun is not None:
                    diag_fun(data, var_names=sub_var_name, coords=sub_coords, ax=ax, **diag_kwargs)
                else:
                    ax.axis("off")
    plt.tight_layout()

In plot_dist_diff, according to the combination of var_names/coords provided, the posteriors of the two parameters are subtracted, and added as a new var_name in data, making the call to plot_posterior simpler (for me)

I maintained the flexibility that the user might provided multiple var_names and want to compare and subtract the posteriors, and that the user knows what they are doing.

So we can have usage like this:

import arviz as az
import matplotlib.pyplot as plt

data = az.load_arviz_data("centered_eight")
az.plot_dist_diff(
	data,
	var_names=['theta'],
	coords={'school': ['Choate', 'Deerfield']},
)

and

az.pair_plot_extended(
	data,
	var_names=["theta"],
	coords={"school": ["Choate", "Deerfield", "Hotchkiss"]},
	upper_fun=az.plot_dist_diff,
	upper_kwargs={'kind': 'hist'},
	lower_kwargs={'plot_kwargs': {'alpha': 0.5}},
    )

and

az.pair_plot_extended(
	data,
	var_names=["theta", "mu"],
	coords={"school": ["Choate", "Deerfield", "Hotchkiss"]},
	upper_fun=None,
	lower_kwargs={'plot_kwargs': {'alpha': 0.5}},
)

Figuring out the lists of all the variables and valid coords is a bit messy here, but it was based off code I found that pair_plot uses.

The labels get a bit messy with so many plots. And (in this example) when a theta is pair_plot-ed with another variable like mu or theta, the coord doesn't get included on the plot.

Is this along the lines of what you were thinking? It's not as quite a simple skeleton as you suggested, but I think it is robust to different types of plots a user might want.

[OriolAbril]

Yes, this definitely follows my line of thought. I will keep playing around with it, to get the most of pairplot and this proposal. It is really good work. I do like the idea of passing xarray datasets, var_names and coords because it will probably allow more options than simply passing the data and the axes. However, it may make the creation of custom plotting functions harder, as it will require understanding xarray and its selection methods.

Do you mind trying this option a little bit and give some feedback? It is extremely similar to the current pair_plot, with some variations:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import NullFormatter
from ..data import convert_to_dataset, convert_to_inference_data
from .plot_utils import _scale_fig_size, xarray_to_ndarray, get_coords
from ..utils import _var_names
from .posteriorplot import plot_posterior
from .pairplot import plot_pair


def plot_func_posterior(data, ax, np_fun=np.diff, **kwargs):
    data = convert_to_dataset(data)
    var_names = [name.replace("\n", "_") for name in data.data_vars]
    func_name = np_fun.__name__
    xlabel = "{}({},\n{})".format(func_name, *var_names)
    data = np_fun(data.to_array(), axis=0).squeeze()
    plot_posterior({xlabel: data}, ax=ax, **kwargs)


def plot_pair_extended(
    data,
    var_names,
    coords=None,
    combined=True,
    lower_fun=plot_pair,
    upper_fun=None,
    diag_fun=plot_posterior,
    lower_kwargs=None,
    upper_kwargs=None,
    diag_kwargs=None,
    figsize=None,
    labels='edges',
    ax=None,
):
    if coords is None:
        coords = {}

    if lower_kwargs is None:
        lower_kwargs = {}

    if upper_kwargs is None:
        upper_kwargs = {}

    if diag_kwargs is None:
        diag_kwargs = {}

    if labels not in ("edges", "all", "none"):
        raise ValueError("labels must be one of (edges, all, none)")

    # Get posterior draws and combine chains
    data = convert_to_inference_data(data)
    posterior_data = convert_to_dataset(data, group="posterior")
    var_names = _var_names(var_names, posterior_data)
    flat_var_names, _posterior = xarray_to_ndarray(
        get_coords(posterior_data, coords), var_names=var_names, combined=combined
    )
    flat_var_names = np.array(flat_var_names)
    numvars = len(flat_var_names)

    (figsize, _, _, _, _, _) = _scale_fig_size(figsize, None, numvars, numvars)
    if ax is None:
        _, ax = plt.subplots(numvars, numvars, figsize=figsize, constrained_layout=True)

    for i in range(numvars):
        for j in range(numvars):
            index = np.array([i, j], dtype=int)
            if i > j:
                if lower_fun is not None:
                    lower_fun(
                        {flat_var_names[j]: _posterior[j], flat_var_names[i]: _posterior[i]},
                        ax=ax[i, j],
                        **lower_kwargs
                    )
                else:
                    ax[i, j].axis("off")
            elif i < j:
                if upper_fun is not None:
                    upper_fun(
                        {flat_var_names[j]: _posterior[j], flat_var_names[i]: _posterior[i]},
                        ax=ax[i, j],
                        **upper_kwargs
                    )
                else:
                    ax[i, j].axis("off")
            elif i == j:
                if diag_fun is not None:
                    diag_fun({flat_var_names[i]: _posterior[i]}, ax=ax[i, j], **diag_kwargs)
                else:
                    ax[i, j].axis("off")


            if (i + 1 != numvars and labels=="edges") or labels=="none":
                ax[i, j].axes.get_xaxis().set_major_formatter(NullFormatter())
                ax[i, j].set_xlabel("")
            if (j != 0 and labels=="edges") or labels=="none":
                ax[i, j].axes.get_yaxis().set_major_formatter(NullFormatter())
                ax[i, j].set_ylabel("")

There also is a kind of wrapper to plot the 1D posterior of a 2 argument function. Its default is np.diff, which gives the same result as plot_dist_diff, but it can be changed to another numpy function or even some custom function.
In plot_pair_extended, I have added some arguments. The combined argument is used to compare different chains when false, and the labels gives some very rough control over the axis labels and ticklabels.

Some examples:

Default behaviour of plot_pair_extended:

az.plot_pair_extended(
    data,
    var_names=["theta"],
    coords={"school": ["Choate", "Deerfield", "Hotchkiss"]},
    figsize=(7,7),
)

Using the wrapper on np.diff as upper_fun:

az.plot_pair_extended(
	data,
	var_names=["theta"],
	coords={"school": ["Choate", "Deerfield", "Hotchkiss"]},
    figsize=(7,7),
    upper_fun=az.plot_func_posterior,
    upper_kwargs={"textsize": 12, "kind":"hist"},
)

Defining a custom plotting function to plot the name of the variables on the diagonal:

def plot_name(data, ax, **kwargs):
    name = list(data.keys())[0]
    ax.text(.5,.5,name,verticalalignment="center",horizontalalignment="center",**kwargs)
    ax.axis('off')
    
az.plot_pair_extended(
    data,
	var_names=["theta"],
	coords={"school": ["Choate", "Deerfield", "Hotchkiss"]},
    diag_fun=plot_name,
    diag_kwargs={"fontsize":17},
    upper_fun=az.plot_pair,
    labels="all",
    figsize=(7,7),
)

This is quite far form what you are interested in, but it is basically to try many different arguments. Comparison between different chains:

az.plot_pair_extended(
    data,
	var_names=["tau"],
	combined=False,
    diag_fun=plot_name,
    diag_kwargs={"fontsize":17},
    upper_fun=az.plot_pair,
    upper_kwargs={"kind":"kde", "fill_last":False},
    lower_kwargs={"plot_kwargs": {"marker":"+","color":"darkblue"}},
    labels="none",
    figsize=(7,7),
)

[hectormz]

This is very nice @OriolAbril ! 👌 So you would be proposing adding both plot_func_posterior and plot_pair_extended to arviZ? I see how plot_func_posterior is being sent a dictionary of the two schools in this case. Could you also show if plot_func_posterior was used alone to create a single difference of posteriors (in this case)?

The customization of labels is very nice. Is there any value of aligning the xlim/ylim for corresponding plots along directions of same variables, or the user would understand that they're not being shown on the same scale (plot_pair and normal plot_posterior in this case)?

It would be nice to reduce the axes grid if only one of the triangles is being shown (and not the diagonal). That can be handled easily while looping through.

[OriolAbril]

Yes, I think that these two could be useful. The plot_name was only for the example. I ended up deciding to pass a dictionary because it can be converted to inference data, which allows to use ArviZ plots, and it is easy to work with, there is only the key which is the label and the item which is the array.

I gave no thought at all to use plot_func_posterior outside pair plot extended, it is quite weird the result as it is now:

data = az.load_arviz_data("centered_eight")
fig, ax = plt.subplots(1,1)
d1 = data.posterior["theta"].sel(school=["Choate"]).to_dict()["data"]
d2 = data.posterior["theta"].sel(school=["Deerfield"]).to_dict()["data"]
az.plot_func_posterior({"Choate":d1, "Deerfield":d2},ax=ax)

I am still thinking about the axis. I have some options in mind, but none of them convince me completely. I think it may be useful to have some argument similar to the labels one, so that when plotting a 2d kde and 1d kde, the axis is shared.

[hectormz]

The dictionary is definitely a clean usage from within pair_plot_extended. Maybe plot_func_posterior could be updated to also receive data like:

data.posterior['theta'].sel({"school":['Choate', 'Deerfield']})

This could be done by modifying plot_func_posterior a little bit:

def plot_func_posterior(data, ax, np_fun=np.diff, **kwargs):
    if isinstance(data, xr.core.dataarray.DataArray):
        var_names, data = xarray_to_ndarray(data)
        data = np_fun(data, axis=0).squeeze()
    else:
        data = convert_to_dataset(data)
        var_names = data.data_vars
        data = np_fun(data.to_array(), axis=0).squeeze()

    var_names = [name.replace("\n", "_") for name in var_names]
    func_name = np_fun.__name__
    xlabel = "{}({},\n{})".format(func_name, *var_names)
    plot_posterior({xlabel: data}, ax=ax, **kwargs)

So:

data = az.load_arviz_data("centered_eight")
fig, ax = plt.subplots(1,1)
az.plot_func_posterior(data.posterior['theta'].sel({"school":['Choate', 'Deerfield']}), ax=ax)

Do you have an idea what other types of functions might be useful to pass to plot_func_posterior?

Sharing the axes is useful, otherwise, hopefully it's obvious to the user when they're not shared (and not labeled). The posterior plots can manage with this if the HPD is displayed.

[OriolAbril]

Do you have an idea what other types of functions might be useful to pass to plot_func_posterior?

I have used the ratio of the inferred variables in some cases.

This is starting to look quite defined! :) Thanks for all the work. I think that now we can start paying attention to presentation and performance. So many conversion from dict to dataset and so on worry me a little.