Reproducing Lucas' Graph Partitioning Example

[seanlaw]

You can check Andrew Lucas' paper on Ising formulations of NP-complete and NP-hard problems, including all of Karp's 21 NP-complete problems.

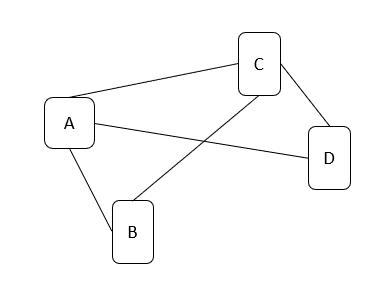
I have been trying to wrap my head around how to formulate other problems into an Ising model so that it can be solved using the simulated bifurcation algorithm. Thus, I started going through each section of Lucas' paper to see if I could solve each type of problem. I was successful with the Number Partitioning problem (section 2.1), which seemed quite straightforward. However, I am now stuck on the Graph Partitioning problem (section 2.2) as it isn't at all clear how to generate the required inputs for SB (namely, the matrix and/or vector). According to Lucas, we start with:

$H=H_A+H_B$

where,

$$H_A=A(\sum^{N}_{n=1}s_i)^2$$

and

$$H_B=B\sum_{(uv) \in E}\frac{1-s_{u}s_{v}}{2}$$

From what I can understand, $H$ should be encompassed by the matrix since both $H_A$ and $H_B$ would be quadratic. My sense is that $H_A$ would be values along the diagonal, however, it's not clear how to incorporate the squaring term after the spins have been summed. Additionally, it isn't clear to me how to encode the $H_B$ into the quadratic matrix at all.

For a more concrete example, let's say we start with the following graph, $G$, with vertices, $V$ and edges, $E$:

According to Lucas, we ask:

what is a partition of the set V into two subsets of equal size N/2 such that the number of edges connecting the two subsets is minimized?

I recognize that given the 4 vertices (A, B, C, D), the objective is to split vertices into two separate groups and where each group is represented by either a positive spin $s_v=+1$ or a negative spin $s_v=-1$. Additionally, given the set of edges that connect the various vertices, $H_B$ acts as a penalty term for breaking an edge by splitting a vertex. However, I still can't seem to figure out how to form the required inputs for SB (i.e., for this example what does $H_A$ and $H_B$ look like? And once I have them, do I simply sum them up into a single matrix and use that in SB?).

Any suggestions or guidance as to how I'd proceed to formulate this for SB would be greatly appreciated. Thanks in advance!

[BusyBeaver-42]

Derivation of $H_A$

My sense is that $H_A$ would be values along the diagonal, however, it's not clear how to incorporate the squaring term after the spins have been summed.

$H_A$ should be a matrix such that for every spin vector $s$, $s^T H_A s = A \left( \displaystyle \sum_{i=1}^N s_i \right)^2.$

Let $\unicode{x1D7D9}$ be the vector of size $N$ whose entries are all $1$'s and let $s$ be a spin vector. First start by rewriting the sum as a dot product:

$$ \displaystyle \sum_{i=1}^N s_i = \unicode{x1D7D9}^T s = s^T \unicode{x1D7D9}. $$

Then using the associativity and the linearity of the matrix product:

$$ A \left( \displaystyle \sum_{i=1}^N s_i \right)^2 = A (s^T \unicode{x1D7D9}) (\unicode{x1D7D9}^T s) = A s^T (\unicode{x1D7D9} \unicode{x1D7D9}^T) s = s^T (A \unicode{x1D7D9} \unicode{x1D7D9}^T) s. $$

Therefore setting $H_A$ to be the $N \times N$ matrix whose elements are all $A$ works:

$$H_A = A \unicode{x1D7D9} \unicode{x1D7D9}^T = \begin{pmatrix} A & \cdots & A \\\ \vdots & \ddots & \vdots \\\ A & \cdots & A \end{pmatrix}.$$

Derivation of $H_B$

In Lucas' paper, the set of edges $E$ contains unordered pairs. This post assumes that $E$ contains ordered pairs. The only thing it changes is that the renormalization factor becomes $\dfrac{1}{4}$ so the energy penalty is $B \displaystyle \sum_{(u, v) \in E} \dfrac{1 - s_u s_v}{4}$.

Note that in the definition of $H_B$, the $\dfrac{1}{4}$ part is constant so it is the same as minimizing $\dfrac{-B}{4} \displaystyle \sum_{(u, v) \in E} s_u s_v$. Let's rewrite this sum as $s^T M s$ for some $N \times N$ matrix $M$.

Let $G$ be the adjacency matrix of the graph, that is $\forall (u,v) \in V^2, (u,v) \in E \implies G_{u,v} = 1 \text{ and } (u,v) \notin E \implies G_{u,v} = 0$. Then, by denoting $(Gs)_u$ the $u$-th entry of the vector $Gs$:

$$ \displaystyle \sum_{(u, v) \in E} s_u s_v = \displaystyle \sum_{u = 1}^N \displaystyle \sum_{v = 1}^N G_{u, v} s_u s_v = \displaystyle \sum_{u = 1}^N s_u \displaystyle \sum_{v = 1}^N G_{u, v} s_v = \displaystyle \sum_{u = 1}^N s_u (Gs)_u = s^T G s. $$

Hence a simple choice for $M$ is the adjacency matrix $G$ of the graph. Then $H_B = \dfrac{-B}{4} G$.

Derivation of $H$

The matrix associated to the sum of two bilinear forms is the sum of the matrices associated to each bilinear form. Hence $H = H_A + H_B$.

Example

For a more concrete example, let's say we start with the following graph, $G$, with vertices, $V$ and edges, $E$:

Let's pick an arbitrary order for the vertices of graph $A: 1, B: 2, C: 3$ and $D:4$. The adjacency matrix of $G$ is

$$M = \begin{pmatrix} 0 & 1 & 1 & 1 \\\ 1 & 0 & 1 & 0 \\\ 1 & 1 & 0 & 1 \\\ 1 & 0 & 1 & 0 \end{pmatrix}.$$

Then $H_B = \dfrac{-B}{4} M$ and

$$H_A = \begin{pmatrix} A & A & A & A \\\ A & A & A & A \\\ A & A & A & A \\\ A & A & A & A \end{pmatrix}.$$

Minimal implementation

Note: this assumes that the adjacency matrix is a numpy array. Also, without loss of generality you can assume that $B = 1$ and only tune the value of $A$.

import numpy as np
import torch
from simulated_bifurcation import SpinPolynomial


class GraphPartioning(SpinPolynomial):
    def __init__(
        self,
        adjacency_matrix: np.ndarray,
        A: float,
        B: float,
        dtype: torch.dtype = torch.float32,
        device: str = "cpu",
    ) -> None:
        adjacency_matrix = torch.tensor(adjacency_matrix, dtype=dtype)
        H_A = torch.full_like(adjacency_matrix, A)
        H_B = -0.25 * B * adjacency_matrix
        matrix = H_A + H_B
        super().__init__(matrix, None, None, dtype, device)

Remarks

I advise setting the value of $\dfrac{A}{B}$ to a larger value than the minimum value $\dfrac{\min(2 \Delta, N)}{8}$ given in Lucas' paper. Indeed the simulated bifurcation is an approximation algorithm so the output may not correspond to an optimal value, just to a spin vector with a low energy.

Also, we are planning to implement more NP-hard / NP-complete problems in the future (we are currently focusing on the documentation, but this is the next step). If you want us to prioritize a specific problem, you can open an issue to request new features (put "[ENH]", standing for "enhancement" at the begining of the title).

[seanlaw]

@BusyBeaver-42 Thank you for your detailed response! I am slowly working my way through the details and I have a question. In Lucas' paper, it was stated that $$H_B=B\sum_{(uv) \in E}\frac{1-s_{u}s_{v}}{2}$$ (note the $1-s_{u}s_{v}$). Maybe I'm not understanding correctly but should this be split into:

$$H_B=B\sum_{(uv) \in E}\frac{1-s_{u}s_{v}}{2}=\frac{B}{2}\sum_{(uv) \in E}1-s_{u}s_{v}=\frac{B}{2}\sum_{(uv) \in E}1-\frac{B}{2}\sum_{(uv) \in E}s_{u}s_{v}$$

Though, it isn't clear to me what constant value $$\sum_{(uv) \in E}1$$ should resolve to? I'm only familiar with seeing the more obvious $$\sum^{N}1=N$$

Also, we are planning to implement more NP-hard / NP-complete problems in the future (we are currently focusing on the documentation, but this is the next step). If you want us to prioritize a specific problem, you can open an issue to request new features (put "[ENH]", standing for "enhancement" at the begining of the title).

I definitely will. For now, I'm trying to familiarize myself with how everything works and to develop a better basic understanding of the underlying SB mechanics. I really appreciate you taking the time and I hope that I can contribute back to the community in the future!

[BusyBeaver-42]

By the way, at first I did not pay attention but in Lucas' paper, the set of edges $E$ contains unordered pairs whereas I wrote the previous post assuming that $E$ contains ordered pairs. The only thing it changes is the renormalization factor: it becomes $\dfrac{1}{4}$ instead of $\dfrac{1}{2}$ (I edited my post).

Denote by $x$ the number of edges in the graph. The sum resolves to $\displaystyle \sum_{(uv) \in E} 1 = x$ (assuming unordered pairs), or $2 x$ (assuming ordered pairs, because each pairs is counted twice: $(u, v)$ and $(v, u)$ ).

[seanlaw]

Ahh, now that I've re-read it and thought about it, I comprehend what you mean when you said that

the 1/4 part is constant so it is the same as minimizing...

Since the constant term itself cannot be minimized (its constant!) and so the only thing that is left is the summation involving $s_us_v$! Thanks for clarifying. I will spend some time go over everything again.

[seanlaw]

@BusyBeaver-42 I'm having some trouble understanding the derivation of $H_B$. Specifically, I understand that $G$ is our full adjacency matrix while $G_{u,v}$ is 1 when an edge exists between vertices $u$ and $v$ and 0 otherwise. What I don't understand is:

$$\sum_{u=1}^Ns_u\sum_{v=1}^NG_{u,v}s_v=\sum_{u=1}^Ns_u(Gs)_u$$

I am failing to grasp how:

$$\sum_{v=1}^NG_{u,v}s_v=(Gs)_u$$

I don't know how to interpret what is actually happening with this summation? What does $(Gs)_u$ mean? Any clarification would be greatly appreciated

[BusyBeaver-42]

The notation $(Gs)_u$ is probably not standard, I should have defined it. The result of the matrix-vector product $Gs$ is another vector, let's call it $y$. I define $(Gs)_u = y_u$ the $u$-th entry of the vector $y$.

The equality

$$\displaystyle \sum_{v=1}^N G_{u,v} s_v = (Gs)_u$$

comes from the definition of the matrix-vector produt.

[seanlaw]

Thanks for the clarification @BusyBeaver-42. Perhaps I'm overthinking/overanalyzing this but I'd like to just talk through it out loud. At the end of the day, $s_uG_{u,v}s_v$ is trying to multiply the spin of vertex $u$ with the presence/absence of an edge between vertices $u$ and $v$ and then finally multiply that with the spin of vertex $v$. There can be only a few combinations:

$s_u$	$G_{u,v}$	$s_v$	$s_uG_{u,v}s_v$
+1	0	+1	0
+1	0	-1	0
+1	1	+1	+1
+1	1	-1	-1
-1	0	+1	0
-1	0	-1	0
-1	1	+1	-1
-1	1	-1	+1

If the resulting multiplication is $s_uG_{u,v}s_v=0$ then nothing happens. When the multiplication is $s_uG_{u,v}s_v=+1$ then both vertices are partitioned to the same "side" (i.e., same spin) and no edge is "broken" (and there is no "cost", i.e., $\frac{1-s_us_v}{2}=0$). However, if the multiplication is $s_uG_{u,v}s_v=-1$ then the two vertices are partitioned on different "sides" and an edge is broken (which results in $\frac{1-s_us_v}{2}=1$). Does that sound about right?

[BusyBeaver-42]

Yes, this is exactly the interpretation of the $H_B$ term without the $B$ factor: it counts the number of broken edges.