| comments | difficulty | edit_url | tags | |||
|---|---|---|---|---|---|---|
true |
Medium |
|
You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
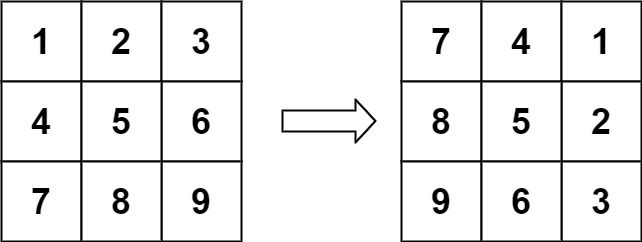
Example 1:
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [[7,4,1],[8,5,2],[9,6,3]]
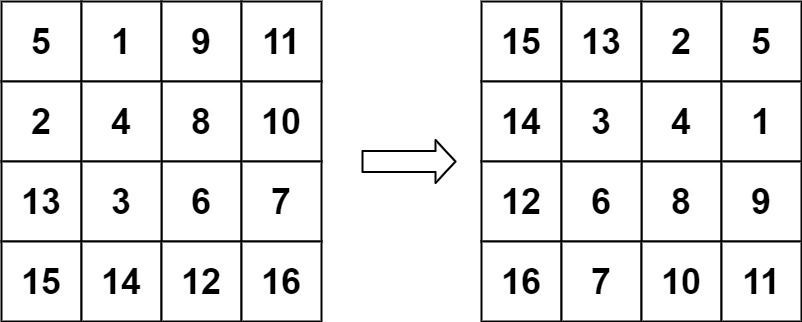
Example 2:
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
According to the problem requirements, we need to rotate
We can first flip the matrix upside down, i.e., swap
The time complexity is
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
n = len(matrix)
for i in range(n >> 1):
for j in range(n):
matrix[i][j], matrix[n - i - 1][j] = matrix[n - i - 1][j], matrix[i][j]
for i in range(n):
for j in range(i):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n >> 1; ++i) {
for (int j = 0; j < n; ++j) {
int t = matrix[i][j];
matrix[i][j] = matrix[n - i - 1][j];
matrix[n - i - 1][j] = t;
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
int t = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = t;
}
}
}
}class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
for (int i = 0; i < n >> 1; ++i) {
for (int j = 0; j < n; ++j) {
swap(matrix[i][j], matrix[n - i - 1][j]);
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
swap(matrix[i][j], matrix[j][i]);
}
}
}
};func rotate(matrix [][]int) {
n := len(matrix)
for i := 0; i < n>>1; i++ {
for j := 0; j < n; j++ {
matrix[i][j], matrix[n-i-1][j] = matrix[n-i-1][j], matrix[i][j]
}
}
for i := 0; i < n; i++ {
for j := 0; j < i; j++ {
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
}
}
}/**
Do not return anything, modify matrix in-place instead.
*/
function rotate(matrix: number[][]): void {
matrix.reverse();
for (let i = 0; i < matrix.length; ++i) {
for (let j = 0; j < i; ++j) {
const t = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = t;
}
}
}impl Solution {
pub fn rotate(matrix: &mut Vec<Vec<i32>>) {
let n = matrix.len();
for i in 0..n / 2 {
for j in 0..n {
let t = matrix[i][j];
matrix[i][j] = matrix[n - i - 1][j];
matrix[n - i - 1][j] = t;
}
}
for i in 0..n {
for j in 0..i {
let t = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = t;
}
}
}
}/**
* @param {number[][]} matrix
* @return {void} Do not return anything, modify matrix in-place instead.
*/
var rotate = function (matrix) {
matrix.reverse();
for (let i = 0; i < matrix.length; ++i) {
for (let j = 0; j < i; ++j) {
[matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
}
}
};public class Solution {
public void Rotate(int[][] matrix) {
int n = matrix.Length;
for (int i = 0; i < n >> 1; ++i) {
for (int j = 0; j < n; ++j) {
int t = matrix[i][j];
matrix[i][j] = matrix[n - i - 1][j];
matrix[n - i - 1][j] = t;
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
int t = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = t;
}
}
}
}