| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
困难 |
|
序列化是指将一个数据结构转化为位序列的过程,因此可以将其存储在文件中或内存缓冲区中,以便稍后在相同或不同的计算机环境中恢复结构。
设计一个序列化和反序列化 N 叉树的算法。一个 N 叉树是指每个节点都有不超过 N 个孩子节点的有根树。序列化 / 反序列化算法的算法实现没有限制。你只需要保证 N 叉树可以被序列化为一个字符串并且该字符串可以被反序列化成原树结构即可。
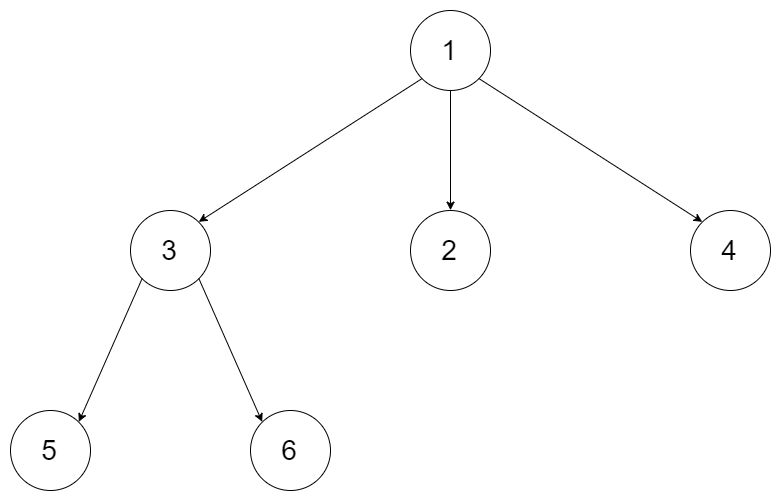
例如,你需要序列化下面的 3-叉 树。
为 [1 [3[5 6] 2 4]]。你不需要以这种形式完成,你可以自己创造和实现不同的方法。
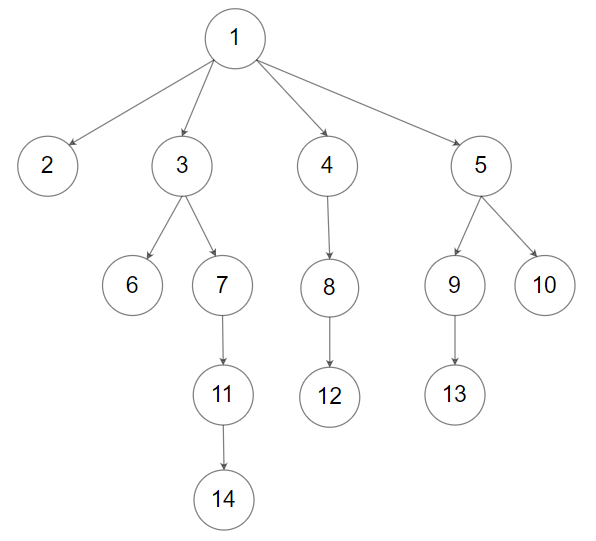
或者,您可以遵循 LeetCode 的层序遍历序列化格式,其中每组孩子节点由空值分隔。
例如,上面的树可以序列化为 [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
你不一定要遵循以上建议的格式,有很多不同的格式,所以请发挥创造力,想出不同的方法来完成本题。
示例 1:
输入: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出: [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
示例 2:
输入: root = [1,null,3,2,4,null,5,6] 输出: [1,null,3,2,4,null,5,6]
示例 3:
输入: root = [] 输出: []
提示:
- 树中节点数目的范围是
[0, 104]. 0 <= Node.val <= 104- N 叉树的高度小于等于
1000 - 不要使用类成员 / 全局变量 / 静态变量来存储状态。你的序列化和反序列化算法应是无状态的。