README.md

comments	difficulty	edit_url	tags
true	简单	https://github.com/doocs/leetcode/edit/main/solution/0500-0599/0559.Maximum%20Depth%20of%20N-ary%20Tree/README.md	树 深度优先搜索 广度优先搜索

559. N 叉树的最大深度

English Version

题目描述

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

 

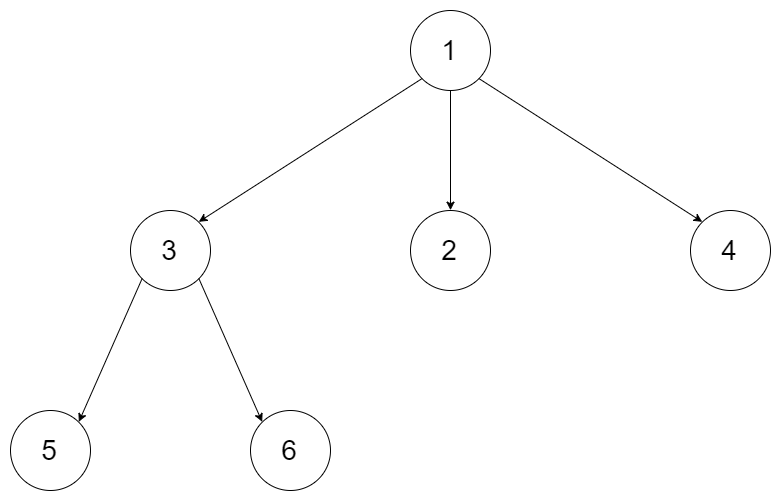
示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：3

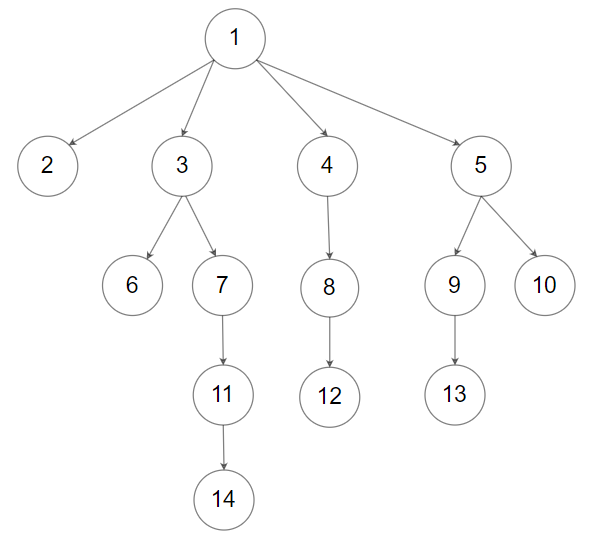
示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

 

提示：

• 树的深度不会超过 1000 。
• 树的节点数目位于 [0, 104] 之间。

解法

方法一：递归

我们首先判断 $\textit{root}$ 是否为空，若为空则返回 0。否则我们初始化一个变量 $\textit{mx}$ 用来记录子节点的最大深度，然后遍历 $\textit{root}$ 的所有子节点，递归调用 $\text{maxDepth}$ 函数，更新 $\textit{mx}$ 的值。最后返回 $\textit{mx} + 1$ 即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为节点的数量。

Python3

"""
# Definition for a Node.
class Node:
    def __init__(self, val: Optional[int] = None, children: Optional[List['Node']] = None):
        self.val = val
        self.children = children
"""


class Solution:
    def maxDepth(self, root: "Node") -> int:
        if root is None:
            return 0
        mx = 0
        for child in root.children:
            mx = max(mx, self.maxDepth(child))
        return 1 + mx

Java

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public int maxDepth(Node root) {
        if (root == null) {
            return 0;
        }
        int mx = 0;
        for (Node child : root.children) {
            mx = Math.max(mx, maxDepth(child));
        }
        return 1 + mx;
    }
}

C++

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        if (!root) {
            return 0;
        }
        int mx = 0;
        for (Node* child : root->children) {
            mx = max(mx, maxDepth(child));
        }
        return mx + 1;
    }
};

Go

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Children []*Node
 * }
 */

func maxDepth(root *Node) int {
	if root == nil {
		return 0
	}
	mx := 0
	for _, child := range root.Children {
		mx = max(mx, maxDepth(child))
	}
	return 1 + mx
}

TypeScript

/**
 * Definition for _Node.
 * class _Node {
 *     val: number
 *     children: _Node[]
 *
 *     constructor(val?: number, children?: _Node[]) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.children = (children===undefined ? [] : children)
 *     }
 * }
 */

function maxDepth(root: _Node | null): number {
    if (!root) {
        return 0;
    }
    return 1 + Math.max(...root.children.map(child => maxDepth(child)), 0);
}