README.md

comments	difficulty	edit_url	tags
true	困难	https://github.com/doocs/leetcode/edit/main/solution/0900-0999/0952.Largest%20Component%20Size%20by%20Common%20Factor/README.md	并查集 数组 哈希表 数学 数论

952. 按公因数计算最大组件大小

English Version

题目描述

给定一个由不同正整数的组成的非空数组 nums ，考虑下面的图：

• 有 nums.length 个节点，按从 nums[0] 到 nums[nums.length - 1] 标记；
• 只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时，nums[i] 和 nums[j]之间才有一条边。

返回 图中最大连通组件的大小 。

 

示例 1：

输入：nums = [4,6,15,35]
输出：4

示例 2：

输入：nums = [20,50,9,63]
输出：2

示例 3：

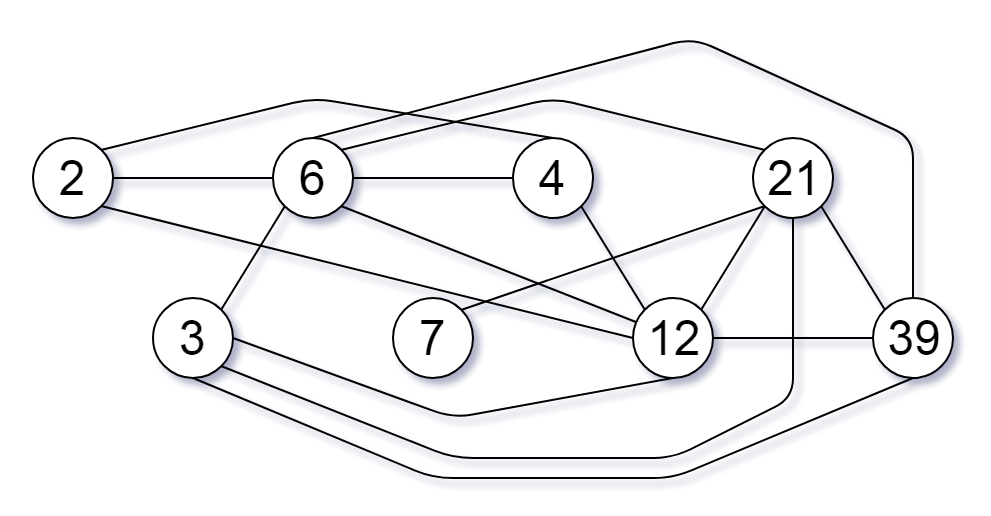
输入：nums = [2,3,6,7,4,12,21,39]
输出：8

 

提示：

• 1 <= nums.length <= 2 * 104
• 1 <= nums[i] <= 105
• nums 中所有值都 不同

解法

方法一：数学 + 并查集

利用“试除法”，对 $nums$ 中的每个数 $v$ 分解因数，然后将每个因数 $i$ 与 $v$ 合并，$v / i$ 与 $v$ 合并。此过程用并查集来维护连通分量。

最后，遍历 $nums$ 中每个数 $v$，找出所在的连通分量，出现次数最多的连通分量就是所求的答案。

Python3

class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))

    def union(self, a, b):
        pa, pb = self.find(a), self.find(b)
        if pa != pb:
            self.p[pa] = pb

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]


class Solution:
    def largestComponentSize(self, nums: List[int]) -> int:
        uf = UnionFind(max(nums) + 1)
        for v in nums:
            i = 2
            while i <= v // i:
                if v % i == 0:
                    uf.union(v, i)
                    uf.union(v, v // i)
                i += 1
        return max(Counter(uf.find(v) for v in nums).values())

Java

class UnionFind {
    int[] p;

    UnionFind(int n) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
    }

    void union(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa != pb) {
            p[pa] = pb;
        }
    }

    int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

class Solution {
    public int largestComponentSize(int[] nums) {
        int m = 0;
        for (int v : nums) {
            m = Math.max(m, v);
        }
        UnionFind uf = new UnionFind(m + 1);
        for (int v : nums) {
            int i = 2;
            while (i <= v / i) {
                if (v % i == 0) {
                    uf.union(v, i);
                    uf.union(v, v / i);
                }
                ++i;
            }
        }
        int[] cnt = new int[m + 1];
        int ans = 0;
        for (int v : nums) {
            int t = uf.find(v);
            ++cnt[t];
            ans = Math.max(ans, cnt[t]);
        }
        return ans;
    }
}

C++

class UnionFind {
public:
    vector<int> p;
    int n;

    UnionFind(int _n)
        : n(_n)
        , p(_n) {
        iota(p.begin(), p.end(), 0);
    }

    void unite(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa != pb) p[pa] = pb;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
};

class Solution {
public:
    int largestComponentSize(vector<int>& nums) {
        int m = *max_element(nums.begin(), nums.end());
        UnionFind* uf = new UnionFind(m + 1);
        for (int v : nums) {
            int i = 2;
            while (i <= v / i) {
                if (v % i == 0) {
                    uf->unite(v, i);
                    uf->unite(v, v / i);
                }
                ++i;
            }
        }
        vector<int> cnt(m + 1);
        int ans = 0;
        for (int v : nums) {
            int t = uf->find(v);
            ++cnt[t];
            ans = max(ans, cnt[t]);
        }
        return ans;
    }
};

Go

func largestComponentSize(nums []int) int {
	m := slices.Max(nums)
	p := make([]int, m+1)
	for i := range p {
		p[i] = i
	}
	var find func(int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	union := func(a, b int) {
		pa, pb := find(a), find(b)
		if pa != pb {
			p[pa] = pb
		}
	}
	for _, v := range nums {
		i := 2
		for i <= v/i {
			if v%i == 0 {
				union(v, i)
				union(v, v/i)
			}
			i++
		}
	}
	cnt := make([]int, m+1)
	for _, v := range nums {
		t := find(v)
		cnt[t]++
	}
	return slices.Max(cnt)
}