| comments | difficulty | edit_url | rating | source | tags | |||||
|---|---|---|---|---|---|---|---|---|---|---|
true |
中等 |
1260 |
第 169 场周赛 Q2 |
|
给你 root1 和 root2 这两棵二叉搜索树。请你返回一个列表,其中包含 两棵树 中的所有整数并按 升序 排序。.
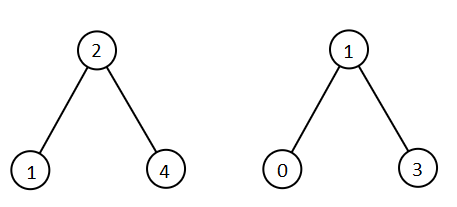
示例 1:
输入:root1 = [2,1,4], root2 = [1,0,3] 输出:[0,1,1,2,3,4]
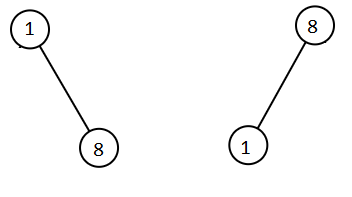
示例 2:
输入:root1 = [1,null,8], root2 = [8,1] 输出:[1,1,8,8]
提示:
- 每棵树的节点数在
[0, 5000]范围内 -105 <= Node.val <= 105
由于两棵树都是二叉搜索树,所以我们可以通过中序遍历得到两棵树的节点值序列
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def getAllElements(
self, root1: Optional[TreeNode], root2: Optional[TreeNode]
) -> List[int]:
def dfs(root: Optional[TreeNode], nums: List[int]) -> int:
if root is None:
return
dfs(root.left, nums)
nums.append(root.val)
dfs(root.right, nums)
a, b = [], []
dfs(root1, a)
dfs(root2, b)
m, n = len(a), len(b)
i = j = 0
ans = []
while i < m and j < n:
if a[i] <= b[j]:
ans.append(a[i])
i += 1
else:
ans.append(b[j])
j += 1
while i < m:
ans.append(a[i])
i += 1
while j < n:
ans.append(b[j])
j += 1
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {
List<Integer> a = new ArrayList<>();
List<Integer> b = new ArrayList<>();
dfs(root1, a);
dfs(root2, b);
int m = a.size(), n = b.size();
int i = 0, j = 0;
List<Integer> ans = new ArrayList<>();
while (i < m && j < n) {
if (a.get(i) <= b.get(j)) {
ans.add(a.get(i++));
} else {
ans.add(b.get(j++));
}
}
while (i < m) {
ans.add(a.get(i++));
}
while (j < n) {
ans.add(b.get(j++));
}
return ans;
}
private void dfs(TreeNode root, List<Integer> nums) {
if (root == null) {
return;
}
dfs(root.left, nums);
nums.add(root.val);
dfs(root.right, nums);
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> getAllElements(TreeNode* root1, TreeNode* root2) {
vector<int> a, b, ans;
dfs(root1, a);
dfs(root2, b);
int i = 0, j = 0;
while (i < a.size() && j < b.size()) {
if (a[i] <= b[j]) {
ans.push_back(a[i++]);
} else {
ans.push_back(b[j++]);
}
}
while (i < a.size()) {
ans.push_back(a[i++]);
}
while (j < b.size()) {
ans.push_back(b[j++]);
}
return ans;
}
private:
void dfs(TreeNode* root, vector<int>& nums) {
if (root == nullptr) {
return;
}
dfs(root->left, nums);
nums.push_back(root->val);
dfs(root->right, nums);
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func getAllElements(root1 *TreeNode, root2 *TreeNode) (ans []int) {
var dfs func(*TreeNode, *[]int)
dfs = func(root *TreeNode, nums *[]int) {
if root == nil {
return
}
dfs(root.Left, nums)
*nums = append(*nums, root.Val)
dfs(root.Right, nums)
}
a, b := []int{}, []int{}
dfs(root1, &a)
dfs(root2, &b)
i, j := 0, 0
m, n := len(a), len(b)
for i < m && j < n {
if a[i] < b[j] {
ans = append(ans, a[i])
i++
} else {
ans = append(ans, b[j])
j++
}
}
for ; i < m; i++ {
ans = append(ans, a[i])
}
for ; j < n; j++ {
ans = append(ans, b[j])
}
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function getAllElements(root1: TreeNode | null, root2: TreeNode | null): number[] {
const dfs = (root: TreeNode | null, nums: number[]) => {
if (!root) {
return;
}
dfs(root.left, nums);
nums.push(root.val);
dfs(root.right, nums);
};
const a: number[] = [];
const b: number[] = [];
dfs(root1, a);
dfs(root2, b);
const [m, n] = [a.length, b.length];
const ans: number[] = [];
let [i, j] = [0, 0];
while (i < m && j < n) {
if (a[i] < b[j]) {
ans.push(a[i++]);
} else {
ans.push(b[j++]);
}
}
while (i < m) {
ans.push(a[i++]);
}
while (j < n) {
ans.push(b[j++]);
}
return ans;
}// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn get_all_elements(
root1: Option<Rc<RefCell<TreeNode>>>,
root2: Option<Rc<RefCell<TreeNode>>>,
) -> Vec<i32> {
let mut a = Vec::new();
let mut b = Vec::new();
Solution::dfs(&root1, &mut a);
Solution::dfs(&root2, &mut b);
let mut ans = Vec::new();
let (mut i, mut j) = (0, 0);
while i < a.len() && j < b.len() {
if a[i] <= b[j] {
ans.push(a[i]);
i += 1;
} else {
ans.push(b[j]);
j += 1;
}
}
while i < a.len() {
ans.push(a[i]);
i += 1;
}
while j < b.len() {
ans.push(b[j]);
j += 1;
}
ans
}
fn dfs(root: &Option<Rc<RefCell<TreeNode>>>, nums: &mut Vec<i32>) {
if let Some(node) = root {
let node = node.borrow();
Solution::dfs(&node.left, nums);
nums.push(node.val);
Solution::dfs(&node.right, nums);
}
}
}