| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
中等 |
1787 |
第 73 场双周赛 Q3 |
|
给你一个正整数 n ,它表示一个 有向无环图 中节点的数目,节点编号为 0 到 n - 1 (包括两者)。
给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。
请你返回一个数组 answer,其中 answer[i]是第 i 个节点的所有 祖先 ,这些祖先节点 升序 排序。
如果 u 通过一系列边,能够到达 v ,那么我们称节点 u 是节点 v 的 祖先 节点。
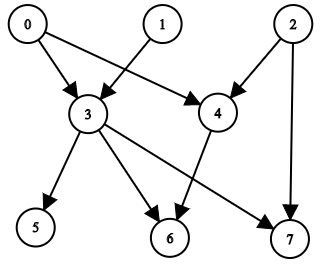
示例 1:
输入:n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]] 输出:[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]] 解释: 上图为输入所对应的图。 - 节点 0 ,1 和 2 没有任何祖先。 - 节点 3 有 2 个祖先 0 和 1 。 - 节点 4 有 2 个祖先 0 和 2 。 - 节点 5 有 3 个祖先 0 ,1 和 3 。 - 节点 6 有 5 个祖先 0 ,1 ,2 ,3 和 4 。 - 节点 7 有 4 个祖先 0 ,1 ,2 和 3 。
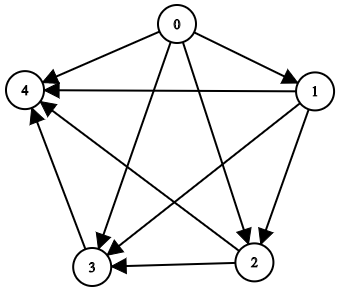
示例 2:
输入:n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]] 输出:[[],[0],[0,1],[0,1,2],[0,1,2,3]] 解释: 上图为输入所对应的图。 - 节点 0 没有任何祖先。 - 节点 1 有 1 个祖先 0 。 - 节点 2 有 2 个祖先 0 和 1 。 - 节点 3 有 3 个祖先 0 ,1 和 2 。 - 节点 4 有 4 个祖先 0 ,1 ,2 和 3 。
提示:
1 <= n <= 10000 <= edges.length <= min(2000, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi <= n - 1fromi != toi- 图中不会有重边。
- 图是 有向 且 无环 的。
我们先根据二维数组
然后我们从小到大枚举节点
时间复杂度
class Solution:
def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:
def bfs(s: int):
q = deque([s])
vis = {s}
while q:
i = q.popleft()
for j in g[i]:
if j not in vis:
vis.add(j)
q.append(j)
ans[j].append(s)
g = defaultdict(list)
for u, v in edges:
g[u].append(v)
ans = [[] for _ in range(n)]
for i in range(n):
bfs(i)
return ansclass Solution {
private int n;
private List<Integer>[] g;
private List<List<Integer>> ans;
public List<List<Integer>> getAncestors(int n, int[][] edges) {
g = new List[n];
this.n = n;
Arrays.setAll(g, i -> new ArrayList<>());
for (var e : edges) {
g[e[0]].add(e[1]);
}
ans = new ArrayList<>();
for (int i = 0; i < n; ++i) {
ans.add(new ArrayList<>());
}
for (int i = 0; i < n; ++i) {
bfs(i);
}
return ans;
}
private void bfs(int s) {
Deque<Integer> q = new ArrayDeque<>();
q.offer(s);
boolean[] vis = new boolean[n];
vis[s] = true;
while (!q.isEmpty()) {
int i = q.poll();
for (int j : g[i]) {
if (!vis[j]) {
vis[j] = true;
q.offer(j);
ans.get(j).add(s);
}
}
}
}
}class Solution {
public:
vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
vector<int> g[n];
for (auto& e : edges) {
g[e[0]].push_back(e[1]);
}
vector<vector<int>> ans(n);
auto bfs = [&](int s) {
queue<int> q;
q.push(s);
bool vis[n];
memset(vis, 0, sizeof(vis));
vis[s] = true;
while (q.size()) {
int i = q.front();
q.pop();
for (int j : g[i]) {
if (!vis[j]) {
vis[j] = true;
ans[j].push_back(s);
q.push(j);
}
}
}
};
for (int i = 0; i < n; ++i) {
bfs(i);
}
return ans;
}
};func getAncestors(n int, edges [][]int) [][]int {
g := make([][]int, n)
for _, e := range edges {
g[e[0]] = append(g[e[0]], e[1])
}
ans := make([][]int, n)
bfs := func(s int) {
q := []int{s}
vis := make([]bool, n)
vis[s] = true
for len(q) > 0 {
i := q[0]
q = q[1:]
for _, j := range g[i] {
if !vis[j] {
vis[j] = true
q = append(q, j)
ans[j] = append(ans[j], s)
}
}
}
}
for i := 0; i < n; i++ {
bfs(i)
}
return ans
}function getAncestors(n: number, edges: number[][]): number[][] {
const g: number[][] = Array.from({ length: n }, () => []);
for (const [u, v] of edges) {
g[u].push(v);
}
const ans: number[][] = Array.from({ length: n }, () => []);
const bfs = (s: number) => {
const q: number[] = [s];
const vis: boolean[] = Array.from({ length: n }, () => false);
vis[s] = true;
while (q.length) {
const i = q.pop()!;
for (const j of g[i]) {
if (!vis[j]) {
vis[j] = true;
ans[j].push(s);
q.push(j);
}
}
}
};
for (let i = 0; i < n; ++i) {
bfs(i);
}
return ans;
}public class Solution {
private int n;
private List<int>[] g;
private IList<IList<int>> ans;
public IList<IList<int>> GetAncestors(int n, int[][] edges) {
g = new List<int>[n];
this.n = n;
for (int i = 0; i < n; i++) {
g[i] = new List<int>();
}
foreach (var e in edges) {
g[e[0]].Add(e[1]);
}
ans = new List<IList<int>>();
for (int i = 0; i < n; ++i) {
ans.Add(new List<int>());
}
for (int i = 0; i < n; ++i) {
BFS(i);
}
return ans;
}
private void BFS(int s) {
Queue<int> q = new Queue<int>();
q.Enqueue(s);
bool[] vis = new bool[n];
vis[s] = true;
while (q.Count > 0) {
int i = q.Dequeue();
foreach (int j in g[i]) {
if (!vis[j]) {
vis[j] = true;
q.Enqueue(j);
ans[j].Add(s);
}
}
}
}
}