| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
中等 |
1472 |
第 292 场周赛 Q2 |
|
给你一棵二叉树的根节点 root ,找出并返回满足要求的节点数,要求节点的值等于其 子树 中值的 平均值 。
注意:
n个元素的平均值可以由n个元素 求和 然后再除以n,并 向下舍入 到最近的整数。root的 子树 由root和它的所有后代组成。
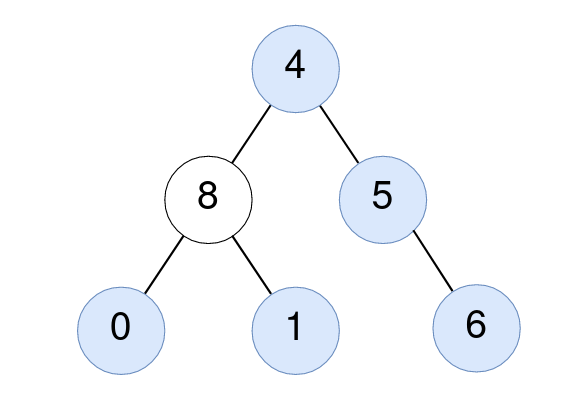
示例 1:
输入:root = [4,8,5,0,1,null,6] 输出:5 解释: 对值为 4 的节点:子树的平均值 (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4 。 对值为 5 的节点:子树的平均值 (5 + 6) / 2 = 11 / 2 = 5 。 对值为 0 的节点:子树的平均值 0 / 1 = 0 。 对值为 1 的节点:子树的平均值 1 / 1 = 1 。 对值为 6 的节点:子树的平均值 6 / 1 = 6 。
示例 2:
输入:root = [1] 输出:1 解释:对值为 1 的节点:子树的平均值 1 / 1 = 1。
提示:
- 树中节点数目在范围
[1, 1000]内 0 <= Node.val <= 1000
我们设计一个函数
函数
- 如果当前节点为空,返回
$(0, 0)$ 。 - 否则,我们递归计算左右子树的和以及节点个数,分别记为
$(\textit{ls}, \textit{ln})$ 和$(\textit{rs}, \textit{rn})$ 。那么,以当前节点为根的子树的和$\textit{s}$ 和节点个数$\textit{n}$ 分别为$\textit{ls} + \textit{rs} + \textit{root.val}$ 和$\textit{ln} + \textit{rn} + 1$ 。如果$\textit{s} / \textit{n} = \textit{root.val}$ ,则说明当前节点满足题目要求,我们将答案$\textit{ans}$ 自增$1$ 。 - 最后,函数
$\textit{dfs}$ 返回$\textit{s}$ 和$\textit{n}$ 。
我们初始化答案
时间复杂度
class Solution:
def averageOfSubtree(self, root: TreeNode) -> int:
def dfs(root) -> tuple:
if not root:
return 0, 0
ls, ln = dfs(root.left)
rs, rn = dfs(root.right)
s = ls + rs + root.val
n = ln + rn + 1
nonlocal ans
ans += int(s // n == root.val)
return s, n
ans = 0
dfs(root)
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans;
public int averageOfSubtree(TreeNode root) {
dfs(root);
return ans;
}
private int[] dfs(TreeNode root) {
if (root == null) {
return new int[2];
}
var l = dfs(root.left);
var r = dfs(root.right);
int s = l[0] + r[0] + root.val;
int n = l[1] + r[1] + 1;
if (s / n == root.val) {
++ans;
}
return new int[] {s, n};
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int averageOfSubtree(TreeNode* root) {
int ans = 0;
auto dfs = [&](this auto&& dfs, TreeNode* root) -> pair<int, int> {
if (!root) {
return {0, 0};
}
auto [ls, ln] = dfs(root->left);
auto [rs, rn] = dfs(root->right);
int s = ls + rs + root->val;
int n = ln + rn + 1;
if (s / n == root->val) {
++ans;
}
return {s, n};
};
dfs(root);
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func averageOfSubtree(root *TreeNode) (ans int) {
var dfs func(root *TreeNode) (int, int)
dfs = func(root *TreeNode) (int, int) {
if root == nil {
return 0, 0
}
ls, ln := dfs(root.Left)
rs, rn := dfs(root.Right)
s, n := ls+rs+root.Val, ln+rn+1
if s/n == root.Val {
ans++
}
return s, n
}
dfs(root)
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function averageOfSubtree(root: TreeNode | null): number {
let ans: number = 0;
const dfs = (root: TreeNode | null): [number, number] => {
if (!root) {
return [0, 0];
}
const [ls, ln] = dfs(root.left);
const [rs, rn] = dfs(root.right);
const s = ls + rs + root.val;
const n = ln + rn + 1;
if (Math.floor(s / n) === root.val) {
++ans;
}
return [s, n];
};
dfs(root);
return ans;
}