| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
中等 |
|
给定一个 下标从 0 开始 的二维整数数组 peaks,其中 peaks[i] = [xi, yi] 表示山 i 在坐标 (xi, yi) 处有一个峰值。山可以被描述为一个直角等腰三角形,它的底部沿着 x 轴,山峰处有一个直角。更正式地说,上山和下山的 梯度 分别为 1 和 -1。
一座山如果它的顶峰不在另一座山 (包括其他山的边界) 之内,那么它被认为是 可见 的。
返回可见山的数量。
示例 1:
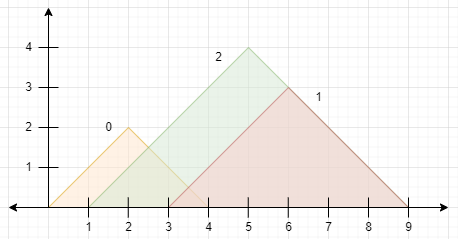
输入: peaks = [[2,2],[6,3],[5,4]] 输出: 2 解释: 上面的图表显示了山脉。 - 山 0 是可见的,因为它的峰值不在另一座山的里面或另一座山的边界。 - 山 1 是不可见的,因为它的顶峰在山 2 的边界。 - 山 2 是可见的,因为它的峰值不在另一座山的里面或另一座山的边界。 有 2 座山是可见的。
示例 2:
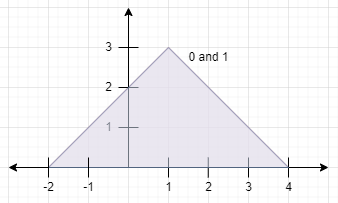
输入: peaks = [[1,3],[1,3]] 输出: 0 解释: 上面的图表显示了这些山 (它们完全重叠)。 两座山都看不见,因为它们的山峰在彼此里面。
提示:
1 <= peaks.length <= 105peaks[i].length == 21 <= xi, yi <= 105
我们先将每座山
接下来,初始化当前区间的右端点为
遍历结束后返回答案即可。
时间复杂度
class Solution:
def visibleMountains(self, peaks: List[List[int]]) -> int:
arr = [(x - y, x + y) for x, y in peaks]
cnt = Counter(arr)
arr.sort(key=lambda x: (x[0], -x[1]))
ans, cur = 0, -inf
for l, r in arr:
if r <= cur:
continue
cur = r
if cnt[(l, r)] == 1:
ans += 1
return ansclass Solution {
public int visibleMountains(int[][] peaks) {
int n = peaks.length;
int[][] arr = new int[n][2];
for (int i = 0; i < n; ++i) {
int x = peaks[i][0], y = peaks[i][1];
arr[i] = new int[] {x - y, x + y};
}
Arrays.sort(arr, (a, b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);
int ans = 0;
int cur = Integer.MIN_VALUE;
for (int i = 0; i < n; ++i) {
int l = arr[i][0], r = arr[i][1];
if (r <= cur) {
continue;
}
cur = r;
if (!(i < n - 1 && arr[i][0] == arr[i + 1][0] && arr[i][1] == arr[i + 1][1])) {
++ans;
}
}
return ans;
}
}class Solution {
public:
int visibleMountains(vector<vector<int>>& peaks) {
vector<pair<int, int>> arr;
for (auto& e : peaks) {
int x = e[0], y = e[1];
arr.emplace_back(x - y, -(x + y));
}
sort(arr.begin(), arr.end());
int n = arr.size();
int ans = 0, cur = INT_MIN;
for (int i = 0; i < n; ++i) {
int l = arr[i].first, r = -arr[i].second;
if (r <= cur) {
continue;
}
cur = r;
ans += i == n - 1 || (i < n - 1 && arr[i] != arr[i + 1]);
}
return ans;
}
};func visibleMountains(peaks [][]int) (ans int) {
n := len(peaks)
type pair struct{ l, r int }
arr := make([]pair, n)
for _, p := range peaks {
x, y := p[0], p[1]
arr = append(arr, pair{x - y, x + y})
}
sort.Slice(arr, func(i, j int) bool { return arr[i].l < arr[j].l || (arr[i].l == arr[j].l && arr[i].r > arr[j].r) })
cur := math.MinInt32
for i, e := range arr {
l, r := e.l, e.r
if r <= cur {
continue
}
cur = r
if !(i < n-1 && l == arr[i+1].l && r == arr[i+1].r) {
ans++
}
}
return
}