| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
中等 |
1908 |
第 125 场双周赛 Q3 |
|
给你一棵无根带权树,树中总共有 n 个节点,分别表示 n 个服务器,服务器从 0 到 n - 1 编号。同时给你一个数组 edges ,其中 edges[i] = [ai, bi, weighti] 表示节点 ai 和 bi 之间有一条双向边,边的权值为 weighti 。再给你一个整数 signalSpeed 。
如果两台服务器 a 和 b 是通过服务器 c 可连接的,则:
a < b,a != c且b != c。- 从
c到a的距离是可以被signalSpeed整除的。 - 从
c到b的距离是可以被signalSpeed整除的。 - 从
c到b的路径与从c到a的路径没有任何公共边。
请你返回一个长度为 n 的整数数组 count ,其中 count[i] 表示通过服务器 i 可连接 的服务器对的 数目 。
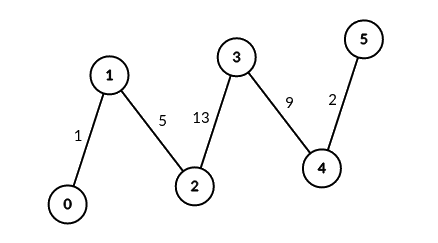
示例 1:
输入:edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1 输出:[0,4,6,6,4,0] 解释:由于 signalSpeed 等于 1 ,count[c] 等于所有从 c 开始且没有公共边的路径对数目。 在输入图中,count[c] 等于服务器 c 左边服务器数目乘以右边服务器数目。
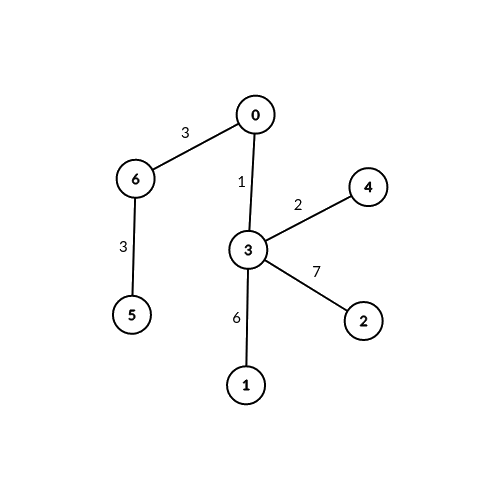
示例 2:
输入:edges = [[0,6,3],[6,5,3],[0,3,1],[3,2,7],[3,1,6],[3,4,2]], signalSpeed = 3 输出:[2,0,0,0,0,0,2] 解释:通过服务器 0 ,有 2 个可连接服务器对(4, 5) 和 (4, 6) 。 通过服务器 6 ,有 2 个可连接服务器对 (4, 5) 和 (0, 5) 。 所有服务器对都必须通过服务器 0 或 6 才可连接,所以其他服务器对应的可连接服务器对数目都为 0 。
提示:
2 <= n <= 1000edges.length == n - 1edges[i].length == 30 <= ai, bi < nedges[i] = [ai, bi, weighti]1 <= weighti <= 1061 <= signalSpeed <= 106- 输入保证
edges构成一棵合法的树。
我们先根据题目给定的边构建出一个邻接表
然后,我们可以枚举每一个节点
枚举完所有节点
时间复杂度
class Solution:
def countPairsOfConnectableServers(
self, edges: List[List[int]], signalSpeed: int
) -> List[int]:
def dfs(a: int, fa: int, ws: int) -> int:
cnt = 0 if ws % signalSpeed else 1
for b, w in g[a]:
if b != fa:
cnt += dfs(b, a, ws + w)
return cnt
n = len(edges) + 1
g = [[] for _ in range(n)]
for a, b, w in edges:
g[a].append((b, w))
g[b].append((a, w))
ans = [0] * n
for a in range(n):
s = 0
for b, w in g[a]:
t = dfs(b, a, w)
ans[a] += s * t
s += t
return ansclass Solution {
private int signalSpeed;
private List<int[]>[] g;
public int[] countPairsOfConnectableServers(int[][] edges, int signalSpeed) {
int n = edges.length + 1;
g = new List[n];
this.signalSpeed = signalSpeed;
Arrays.setAll(g, k -> new ArrayList<>());
for (var e : edges) {
int a = e[0], b = e[1], w = e[2];
g[a].add(new int[] {b, w});
g[b].add(new int[] {a, w});
}
int[] ans = new int[n];
for (int a = 0; a < n; ++a) {
int s = 0;
for (var e : g[a]) {
int b = e[0], w = e[1];
int t = dfs(b, a, w);
ans[a] += s * t;
s += t;
}
}
return ans;
}
private int dfs(int a, int fa, int ws) {
int cnt = ws % signalSpeed == 0 ? 1 : 0;
for (var e : g[a]) {
int b = e[0], w = e[1];
if (b != fa) {
cnt += dfs(b, a, ws + w);
}
}
return cnt;
}
}class Solution {
public:
vector<int> countPairsOfConnectableServers(vector<vector<int>>& edges, int signalSpeed) {
int n = edges.size() + 1;
vector<pair<int, int>> g[n];
for (auto& e : edges) {
int a = e[0], b = e[1], w = e[2];
g[a].emplace_back(b, w);
g[b].emplace_back(a, w);
}
function<int(int, int, int)> dfs = [&](int a, int fa, int ws) {
int cnt = ws % signalSpeed == 0;
for (auto& [b, w] : g[a]) {
if (b != fa) {
cnt += dfs(b, a, ws + w);
}
}
return cnt;
};
vector<int> ans(n);
for (int a = 0; a < n; ++a) {
int s = 0;
for (auto& [b, w] : g[a]) {
int t = dfs(b, a, w);
ans[a] += s * t;
s += t;
}
}
return ans;
}
};func countPairsOfConnectableServers(edges [][]int, signalSpeed int) []int {
n := len(edges) + 1
type pair struct{ x, w int }
g := make([][]pair, n)
for _, e := range edges {
a, b, w := e[0], e[1], e[2]
g[a] = append(g[a], pair{b, w})
g[b] = append(g[b], pair{a, w})
}
var dfs func(a, fa, ws int) int
dfs = func(a, fa, ws int) int {
cnt := 0
if ws%signalSpeed == 0 {
cnt++
}
for _, e := range g[a] {
b, w := e.x, e.w
if b != fa {
cnt += dfs(b, a, ws+w)
}
}
return cnt
}
ans := make([]int, n)
for a := 0; a < n; a++ {
s := 0
for _, e := range g[a] {
b, w := e.x, e.w
t := dfs(b, a, w)
ans[a] += s * t
s += t
}
}
return ans
}function countPairsOfConnectableServers(edges: number[][], signalSpeed: number): number[] {
const n = edges.length + 1;
const g: [number, number][][] = Array.from({ length: n }, () => []);
for (const [a, b, w] of edges) {
g[a].push([b, w]);
g[b].push([a, w]);
}
const dfs = (a: number, fa: number, ws: number): number => {
let cnt = ws % signalSpeed === 0 ? 1 : 0;
for (const [b, w] of g[a]) {
if (b != fa) {
cnt += dfs(b, a, ws + w);
}
}
return cnt;
};
const ans: number[] = Array(n).fill(0);
for (let a = 0; a < n; ++a) {
let s = 0;
for (const [b, w] of g[a]) {
const t = dfs(b, a, w);
ans[a] += s * t;
s += t;
}
}
return ans;
}