| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
中等 |
1689 |
第 387 场周赛 Q3 |
|
给你一个下标从 0 开始、大小为 n x n 的矩阵 grid ,其中 n 为奇数,且 grid[r][c] 的值为 0 、1 或 2 。
如果一个单元格属于以下三条线中的任一一条,我们就认为它是字母 Y 的一部分:
- 从左上角单元格开始到矩阵中心单元格结束的对角线。
- 从右上角单元格开始到矩阵中心单元格结束的对角线。
- 从中心单元格开始到矩阵底部边界结束的垂直线。
当且仅当满足以下全部条件时,可以判定矩阵上写有字母 Y :
- 属于 Y 的所有单元格的值相等。
- 不属于 Y 的所有单元格的值相等。
- 属于 Y 的单元格的值与不属于Y的单元格的值不同。
每次操作你可以将任意单元格的值改变为 0 、1 或 2 。返回在矩阵上写出字母 Y 所需的 最少 操作次数。
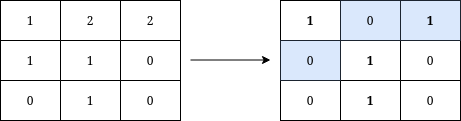
示例 1:
输入:grid = [[1,2,2],[1,1,0],[0,1,0]] 输出:3 解释:将在矩阵上写出字母 Y 需要执行的操作用蓝色高亮显示。操作后,所有属于 Y 的单元格(加粗显示)的值都为 1 ,而不属于 Y 的单元格的值都为 0 。 可以证明,写出 Y 至少需要进行 3 次操作。
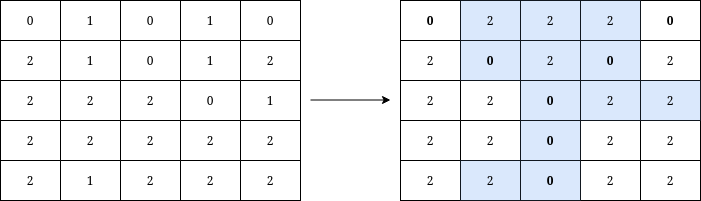
示例 2:
输入:grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]] 输出:12 解释:将在矩阵上写出字母 Y 需要执行的操作用蓝色高亮显示。操作后,所有属于 Y 的单元格(加粗显示)的值都为 0 ,而不属于 Y 的单元格的值都为 2 。 可以证明,写出 Y 至少需要进行 12 次操作。
提示:
3 <= n <= 49n == grid.length == grid[i].length0 <= grid[i][j] <= 2n为奇数。
我们用两个长度为 cnt1 和 cnt2 分别记录属于 Y 的单元格和不属于 Y 的单元格的值的个数。然后我们枚举 i 和 j,分别表示属于 Y 的单元格和不属于 Y 的单元格的值,计算出最少操作次数。
时间复杂度
class Solution:
def minimumOperationsToWriteY(self, grid: List[List[int]]) -> int:
n = len(grid)
cnt1 = Counter()
cnt2 = Counter()
for i, row in enumerate(grid):
for j, x in enumerate(row):
a = i == j and i <= n // 2
b = i + j == n - 1 and i <= n // 2
c = j == n // 2 and i >= n // 2
if a or b or c:
cnt1[x] += 1
else:
cnt2[x] += 1
return min(
n * n - cnt1[i] - cnt2[j] for i in range(3) for j in range(3) if i != j
)class Solution {
public int minimumOperationsToWriteY(int[][] grid) {
int n = grid.length;
int[] cnt1 = new int[3];
int[] cnt2 = new int[3];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
boolean a = i == j && i <= n / 2;
boolean b = i + j == n - 1 && i <= n / 2;
boolean c = j == n / 2 && i >= n / 2;
if (a || b || c) {
++cnt1[grid[i][j]];
} else {
++cnt2[grid[i][j]];
}
}
}
int ans = n * n;
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
if (i != j) {
ans = Math.min(ans, n * n - cnt1[i] - cnt2[j]);
}
}
}
return ans;
}
}class Solution {
public:
int minimumOperationsToWriteY(vector<vector<int>>& grid) {
int n = grid.size();
int cnt1[3]{};
int cnt2[3]{};
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
bool a = i == j && i <= n / 2;
bool b = i + j == n - 1 && i <= n / 2;
bool c = j == n / 2 && i >= n / 2;
if (a || b || c) {
++cnt1[grid[i][j]];
} else {
++cnt2[grid[i][j]];
}
}
}
int ans = n * n;
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
if (i != j) {
ans = min(ans, n * n - cnt1[i] - cnt2[j]);
}
}
}
return ans;
}
};func minimumOperationsToWriteY(grid [][]int) int {
n := len(grid)
cnt1 := [3]int{}
cnt2 := [3]int{}
for i, row := range grid {
for j, x := range row {
a := i == j && i <= n/2
b := i+j == n-1 && i <= n/2
c := j == n/2 && i >= n/2
if a || b || c {
cnt1[x]++
} else {
cnt2[x]++
}
}
}
ans := n * n
for i := 0; i < 3; i++ {
for j := 0; j < 3; j++ {
if i != j {
ans = min(ans, n*n-cnt1[i]-cnt2[j])
}
}
}
return ans
}function minimumOperationsToWriteY(grid: number[][]): number {
const n = grid.length;
const cnt1: number[] = Array(3).fill(0);
const cnt2: number[] = Array(3).fill(0);
for (let i = 0; i < n; ++i) {
for (let j = 0; j < n; ++j) {
const a = i === j && i <= n >> 1;
const b = i + j === n - 1 && i <= n >> 1;
const c = j === n >> 1 && i >= n >> 1;
if (a || b || c) {
++cnt1[grid[i][j]];
} else {
++cnt2[grid[i][j]];
}
}
}
let ans = n * n;
for (let i = 0; i < 3; ++i) {
for (let j = 0; j < 3; ++j) {
if (i !== j) {
ans = Math.min(ans, n * n - cnt1[i] - cnt2[j]);
}
}
}
return ans;
}