| comments | difficulty | edit_url | rating | source | tags | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
true |
困难 |
2454 |
第 420 场周赛 Q4 |
|
给你一棵 n 个节点的树,树的根节点为 0 ,n 个节点的编号为 0 到 n - 1 。这棵树用一个长度为 n 的数组 parent 表示,其中 parent[i] 是节点 i 的父节点。由于节点 0 是根节点,所以 parent[0] == -1 。
给你一个长度为 n 的字符串 s ,其中 s[i] 是节点 i 对应的字符。
一开始你有一个空字符串 dfsStr ,定义一个递归函数 dfs(int x) ,它的输入是节点 x ,并依次执行以下操作:
- 按照 节点编号升序 遍历
x的所有孩子节点y,并调用dfs(y)。 - 将 字符
s[x]添加到字符串dfsStr的末尾。
注意,所有递归函数 dfs 都共享全局变量 dfsStr 。
你需要求出一个长度为 n 的布尔数组 answer ,对于 0 到 n - 1 的每一个下标 i ,你需要执行以下操作:
- 清空字符串
dfsStr并调用dfs(i)。 - 如果结果字符串
dfsStr是一个 回文串 ,answer[i]为true,否则answer[i]为false。
请你返回字符串 answer 。
示例 1:
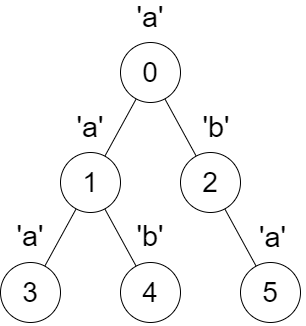
输入:parent = [-1,0,0,1,1,2], s = "aababa"
输出:[true,true,false,true,true,true]
解释:
- 调用
dfs(0),得到字符串dfsStr = "abaaba",是一个回文串。 - 调用
dfs(1),得到字符串dfsStr = "aba",是一个回文串。 - 调用
dfs(2),得到字符串dfsStr = "ab",不 是回文串。 - 调用
dfs(3),得到字符串dfsStr = "a",是一个回文串。 - 调用
dfs(4),得到字符串dfsStr = "b",是一个回文串。 - 调用
dfs(5),得到字符串dfsStr = "a",是一个回文串。
示例 2:
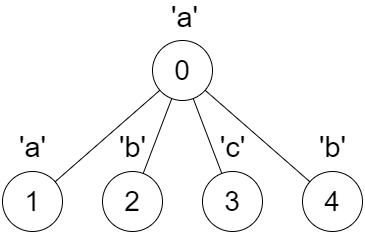
输入:parent = [-1,0,0,0,0], s = "aabcb"
输出:[true,true,true,true,true]
解释:
每一次调用 dfs(x) 都得到一个回文串。
提示:
n == parent.length == s.length1 <= n <= 105- 对于所有
i >= 1,都有0 <= parent[i] <= n - 1。 parent[0] == -1parent表示一棵合法的树。s只包含小写英文字母。
我们可以使用深度优先搜索(DFS)来遍历树,将整棵树的
然后我们使用字符串哈希的方法,分别求出
时间复杂度
class Hashing:
__slots__ = ["mod", "h", "p"]
def __init__(self, s: List[str], base: int, mod: int):
self.mod = mod
self.h = [0] * (len(s) + 1)
self.p = [1] * (len(s) + 1)
for i in range(1, len(s) + 1):
self.h[i] = (self.h[i - 1] * base + ord(s[i - 1])) % mod
self.p[i] = (self.p[i - 1] * base) % mod
def query(self, l: int, r: int) -> int:
return (self.h[r] - self.h[l - 1] * self.p[r - l + 1]) % self.mod
class Solution:
def findAnswer(self, parent: List[int], s: str) -> List[bool]:
def dfs(i: int):
l = len(dfsStr) + 1
for j in g[i]:
dfs(j)
dfsStr.append(s[i])
r = len(dfsStr)
pos[i] = (l, r)
n = len(s)
g = [[] for _ in range(n)]
for i in range(1, n):
g[parent[i]].append(i)
dfsStr = []
pos = {}
dfs(0)
base, mod = 13331, 998244353
h1 = Hashing(dfsStr, base, mod)
h2 = Hashing(dfsStr[::-1], base, mod)
ans = []
for i in range(n):
l, r = pos[i]
k = r - l + 1
v1 = h1.query(l, l + k // 2 - 1)
v2 = h2.query(n - r + 1, n - r + 1 + k // 2 - 1)
ans.append(v1 == v2)
return ansclass Hashing {
private final long[] p;
private final long[] h;
private final long mod;
public Hashing(String word, long base, int mod) {
int n = word.length();
p = new long[n + 1];
h = new long[n + 1];
p[0] = 1;
this.mod = mod;
for (int i = 1; i <= n; i++) {
p[i] = p[i - 1] * base % mod;
h[i] = (h[i - 1] * base + word.charAt(i - 1)) % mod;
}
}
public long query(int l, int r) {
return (h[r] - h[l - 1] * p[r - l + 1] % mod + mod) % mod;
}
}
class Solution {
private char[] s;
private int[][] pos;
private List<Integer>[] g;
private StringBuilder dfsStr = new StringBuilder();
public boolean[] findAnswer(int[] parent, String s) {
this.s = s.toCharArray();
int n = s.length();
g = new List[n];
pos = new int[n][0];
Arrays.setAll(g, k -> new ArrayList<>());
for (int i = 1; i < n; ++i) {
g[parent[i]].add(i);
}
dfs(0);
final int base = 13331;
final int mod = 998244353;
Hashing h1 = new Hashing(dfsStr.toString(), base, mod);
Hashing h2 = new Hashing(new StringBuilder(dfsStr).reverse().toString(), base, mod);
boolean[] ans = new boolean[n];
for (int i = 0; i < n; ++i) {
int l = pos[i][0], r = pos[i][1];
int k = r - l + 1;
long v1 = h1.query(l, l + k / 2 - 1);
long v2 = h2.query(n + 1 - r, n + 1 - r + k / 2 - 1);
ans[i] = v1 == v2;
}
return ans;
}
private void dfs(int i) {
int l = dfsStr.length() + 1;
for (int j : g[i]) {
dfs(j);
}
dfsStr.append(s[i]);
int r = dfsStr.length();
pos[i] = new int[] {l, r};
}
}class Hashing {
private:
vector<long long> p;
vector<long long> h;
long long mod;
public:
Hashing(string word, long long base, int mod) {
int n = word.size();
p.resize(n + 1);
h.resize(n + 1);
p[0] = 1;
this->mod = mod;
for (int i = 1; i <= n; i++) {
p[i] = (p[i - 1] * base) % mod;
h[i] = (h[i - 1] * base + word[i - 1] - 'a') % mod;
}
}
long long query(int l, int r) {
return (h[r] - h[l - 1] * p[r - l + 1] % mod + mod) % mod;
}
};
class Solution {
public:
vector<bool> findAnswer(vector<int>& parent, string s) {
int n = s.size();
vector<int> g[n];
for (int i = 1; i < n; ++i) {
g[parent[i]].push_back(i);
}
string dfsStr;
vector<pair<int, int>> pos(n);
auto dfs = [&](this auto&& dfs, int i) -> void {
int l = dfsStr.size() + 1;
for (int j : g[i]) {
dfs(j);
}
dfsStr.push_back(s[i]);
int r = dfsStr.size();
pos[i] = {l, r};
};
dfs(0);
const int base = 13331;
const int mod = 998244353;
Hashing h1(dfsStr, base, mod);
reverse(dfsStr.begin(), dfsStr.end());
Hashing h2(dfsStr, base, mod);
vector<bool> ans(n);
for (int i = 0; i < n; ++i) {
auto [l, r] = pos[i];
int k = r - l + 1;
long long v1 = h1.query(l, l + k / 2 - 1);
long long v2 = h2.query(n - r + 1, n - r + 1 + k / 2 - 1);
ans[i] = v1 == v2;
}
return ans;
}
};type Hashing struct {
p []int64
h []int64
mod int64
}
func NewHashing(word string, base, mod int64) *Hashing {
n := len(word)
p := make([]int64, n+1)
h := make([]int64, n+1)
p[0] = 1
for i := 1; i <= n; i++ {
p[i] = p[i-1] * base % mod
h[i] = (h[i-1]*base + int64(word[i-1])) % mod
}
return &Hashing{p, h, mod}
}
func (hs *Hashing) query(l, r int) int64 {
return (hs.h[r] - hs.h[l-1]*hs.p[r-l+1]%hs.mod + hs.mod) % hs.mod
}
func findAnswer(parent []int, s string) (ans []bool) {
n := len(s)
g := make([][]int, n)
for i := 1; i < n; i++ {
g[parent[i]] = append(g[parent[i]], i)
}
dfsStr := []byte{}
pos := make([][2]int, n)
var dfs func(int)
dfs = func(i int) {
l := len(dfsStr) + 1
for _, j := range g[i] {
dfs(j)
}
dfsStr = append(dfsStr, s[i])
r := len(dfsStr)
pos[i] = [2]int{l, r}
}
const base = 13331
const mod = 998244353
dfs(0)
h1 := NewHashing(string(dfsStr), base, mod)
for i, j := 0, len(dfsStr)-1; i < j; i, j = i+1, j-1 {
dfsStr[i], dfsStr[j] = dfsStr[j], dfsStr[i]
}
h2 := NewHashing(string(dfsStr), base, mod)
for i := 0; i < n; i++ {
l, r := pos[i][0], pos[i][1]
k := r - l + 1
v1 := h1.query(l, l+k/2-1)
v2 := h2.query(n-r+1, n-r+1+k/2-1)
ans = append(ans, v1 == v2)
}
return
}