Hard Neumman Constraints - Help with a particular case

[JPlataSalas]

Hello dear Community and Lu,

First of all, thank you for the hard work you made creating DeepXDE.

Second, I am starting to use DeepXDE, so I'm testing "simple" examples to verify its operation.

The particular case (one-dimensional) that I'm solving the equation:

$$ \frac{d^2}{dx^2} \left( E I(x) \frac{d^2 W}{dx^2} \right) + p \frac{d^2 W}{dx^2} = 0 $$

With (Dirichlet/Neumman) conditions:
$$W(x=0) = W(x = L) = 0$$

$$W'(x=0) = W'(x=L) = 0$$

First, trying to solve:

$$ I(x) = I_0 $$

y $$I(x) = I_0 + g(x)$$.

Well, I implemented the equation above using DeepXDE (code attached);

deepxde_code.txt

I have read the FAQ forum and I found the way to fix a hard constraint for Dirichlet conditions, nevertheless, I couldn't make it for Neumann conditions. For this case, I believe that I'm not implementing the equation correctly since I'm not obtaining the "theorical plots". The first indication of fail is that the plot doesn't show that its derivate is zero at borders.

Results:

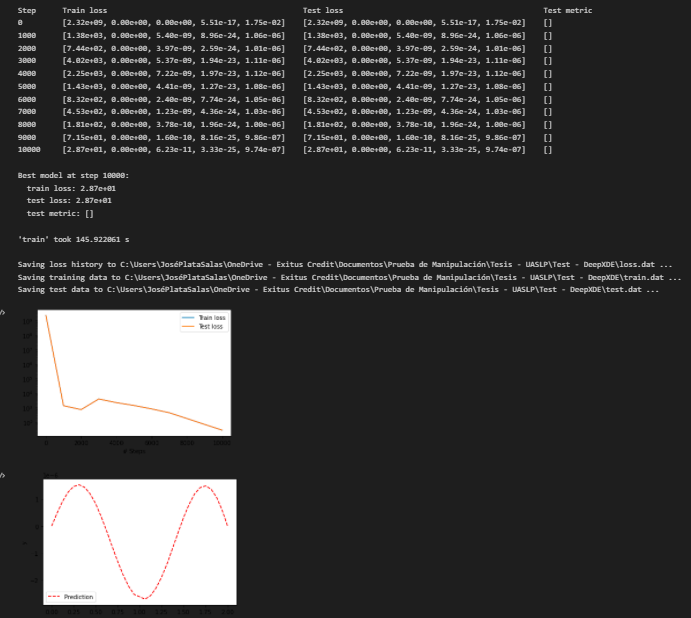
In particular, I'm trying to recreate the plots from this papers:

qiu2004.pdf

Can you help me with some suggestions so I can solve this and other equations, please?

Thank in advance for your help,

Jose

[lululxvi]

See paper: Systematic Construction of Neural Forms for Solving Partial Differential Equations Inside Rectangular Domains, Subject to Initial, Boundary and Interface Conditions.