Wearable Sensor for Spine Movement

General Information about this Project

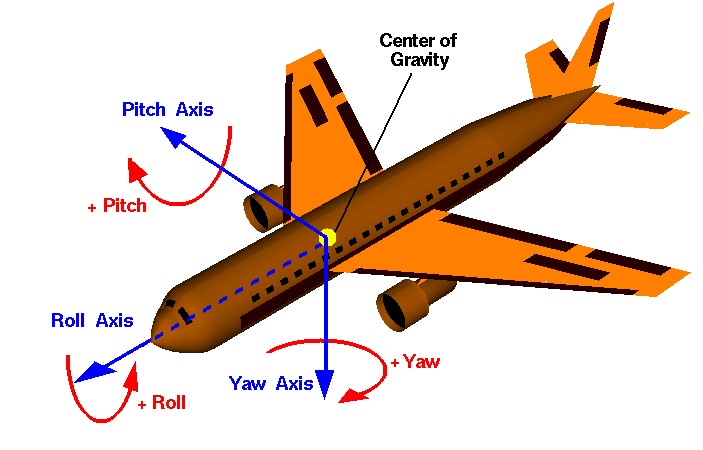
• Goal: Using two IMU sensors (in red) placed on the spine to monitor the spinal motion and curvature.

  

• We've done some previous work to have the IMU sensors measure the rotational angles on the x, y, z axis. The angles of rotation are called roll, pitch, yaw, respectfully.

  

Simulating the Spine Curve

0. Some Background Knowledge -- Bezier Curve

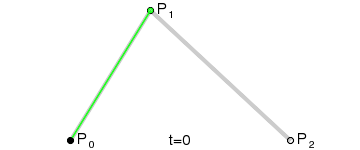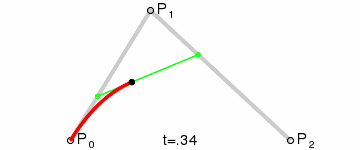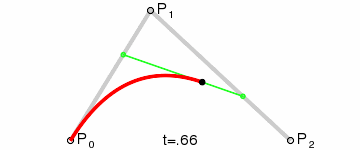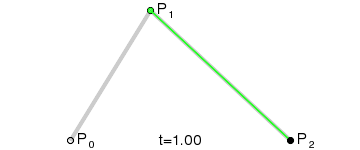
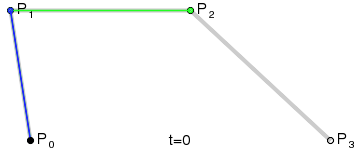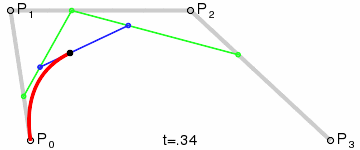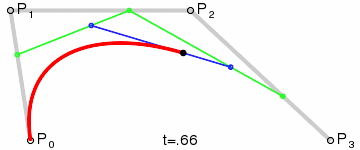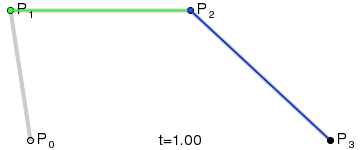
• What it is: Parametric Curves defined by a set of control points

• How the curves are drawn:

  • 3 control points in 2D:

    

  • 4 control points in 2D:

    

• Mathematical Definition:

  • The general formula of Bézier curve $ \mathbf{B}(t) $ is given by:

    $$ \mathbf{B}(t) = \sum_{i=0}^{n} \binom{n}{i} (1 - t)^{n-i} t^i \mathbf{P}_i $$ where t describes the position of the points along the curve, range from 0 to 1.

  • The formula can be expanded as:

    $$ \mathbf{B}(t) = (1 - t)^n \mathbf{P}_0 + \binom{n}{1} (1 - t)^{n-1} t \mathbf{P}_1 + \cdots + \binom{n}{n-1} (1 - t) t^{n-1} \mathbf{P}_{n-1} + t^n \mathbf{P}_n, \quad 0 \leq t \leq 1 $$

  • The derivative: $$ \mathbf{B}'(t) = n \sum_{i=0}^{n-1} b_{i,n-1}(t) (\mathbf{P}_{i+1} - \mathbf{P}_i), \quad 0 \leq t \leq 1 $$

1. Defining Our Problem Space

• We aim to simulate the curvature of the spine based on IMU readings.

  Uncertainty 1: I thought that we would have enough information to draw a 4-point Bezier curve yet this might not be true. If this turns out to be causing the issue, I would gladly turn the order of the curve to 3-points.

• For simplification, we treat the selected spine segment as a curved path defined by four control points: A, B, C, and D, with IMUs placed at positions corresponding to 20% and 80% along the path.

  t1 = 0.2, t2 = 0.8
  

  

• We define the start and end points of the path, A and D, which gives us two points to start with. Then, we work backwards using properties derived from the IMU readings to determine the coordinates of the intermediate control points B and C.

• To summerize the given and unknowns:

  • Given:
    1. The IMU readings roll, pitch, yaw at two positions along the curve.
    2. The distances or relative positions of the IMUs (20% and 80% along the curve).
    3. The coordinates of the start and end points, A and D.
       • (the coordinates can be anything, I just happened to be picking (0, 2.5, 0) and (0, -2.5,0) for simplicity of graphing, we can change this)
  • To find: The coordinates of the intermediate control points B and C.

2. Thought Process in Solving the Problem

• For a 4-point Bezier Curve with points, $ \mathbf n=4 $, the equation with respect to the four points A, B, C,D is given by:

  $$ \mathbf{B}(t) = (1-t)^3\mathbf{A}+3(1-t)^2t\mathbf{B}+3(1-t)t^2\mathbf{C}+t^3\mathbf{D},\ 0 \le t \le 1 $$

  with derivative:

  $$ \frac{d\mathbf{B}}{dt} = -3(1 - t)^2 \mathbf{A} + 3(1 - t)(1 - 3t) \mathbf{B} + 3t(2 - 3t) \mathbf{C} + 3t^2 \mathbf{D} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (*) $$

• Here, A and D are known.

• If we are able to get $ \frac{d\mathbf{B}}{dt} $ at $ \mathbf t=0.2, t=0.8 $ through the row, pitch, yaw angles provided by the two IMUs, then the only unknows we are left with will be B, and C.

• We should then be able to solve the problem by solving the two quadratic equations at $ \mathbf t=0.2, t=0.8 $

  Uncertainty 2: The assumption made in here was that the row, pitch, yaw angles we got from the IMU sensors will give us enough information to construct dB/dt, yet this might be false.

3. Current Attempt / Work in Solving the Problem

step 1: Turning roll, pitch, yaw angles from each sensor into $\frac{d\mathbf{B}}{dt}$

1. Construct a rotational matrix from the elementry rotation on each idividual axis

2. Multiple the rotation matrix with a basis vector: $$ \mathbf{v}_{\text{rotated}} = R \cdot \mathbf{v},\ \
   v = \begin{bmatrix} 1 \ 0 \ 0 \end{bmatrix} $$`

3. I then used $\mathbf{v}_{\text{rotated}}$ as the gradient vector $\frac {d\mathbf{B}}{dt}$

   Uncertainty 3: I'm aware that this step may be wrong but I don't know how to fix it: the roll, pitch, yaw angles gives only the direction of the gradient vector but not the magnitude. I tried normalizing the gradient vector got from this step and use it as dB/dt, but it did't work out and made no logical sense.

step 2: Solving for B and C knowing A, D, $\frac{d\mathbf{B}}{dt}$

1. pluged in $ t = 0.2 $ and $ t=0.8 $ into equation $(*)$

   

2. Solved B and C using matrices:

   

4. Current (irrational) Results

• right now, when I test my code by setting the roll, pitch, yaw angles as shown in the picture:

  

  the gradient vector $\frac {d\mathbf{B}}{dt}$ I got for t = 0.2 and 0.8 are:

  

  the final answer calculated for vector B and C are:

  
  • This answer is way off, because given the start point and end point, the y-axis value for B and C should be within [-2.5, 2.5].