---

BoFire — Bayesian Optimization Framework Intended for Real Experiments

BoFire is a powerful Python package that serves as a comprehensive framework for experimental design. BoFire is designed to empower researchers, data scientists, engineers, and enthusiasts who are venturing into the world of Design of Experiments (DoE) and Bayesian optimization (BO) techniques.

Why BoFire? BoFire ...

• supports mixed continuous, discrete and categorical parameter spaces for system inputs and outputs,
• separates objectives (minimize, maximize, close-to-target) from the outputs on which they operate,
• supports different specific and generic constraints as well as black-box output constraints,
• can provide flexible DoEs that fulfill constraints,
• provides sampling methods for constrained mixed variable spaces,
• serializes problems for use in RESTful APIs and json/bson DBs, and
• allows easy out of the box usage of strategies for single and multi-objective Bayesian optimization.

Getting started

In our docs, you can find all different options for the BoFire installation. For basic BoFire Bayesian optimization features using BoTorch which depends on PyTorch, you need to run

pip install bofire[optimization]

For a more complete introduction to BoFire, please look in our docs.

Optimization problem

You will find a notebook covering the described example below in our tutorials section to run the code yourself.

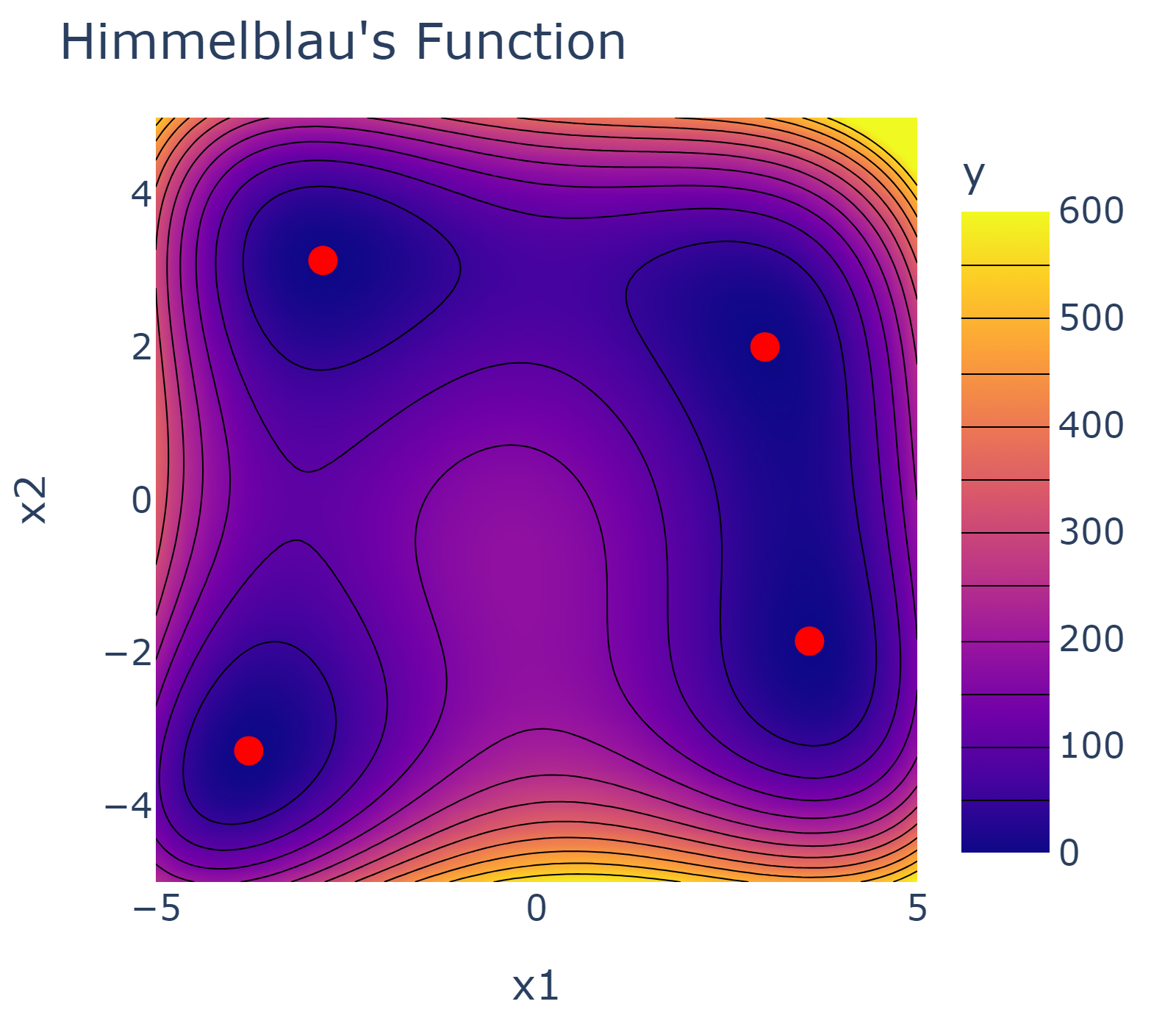
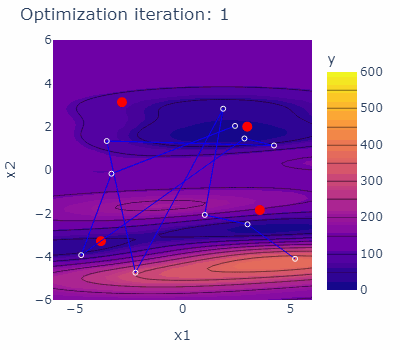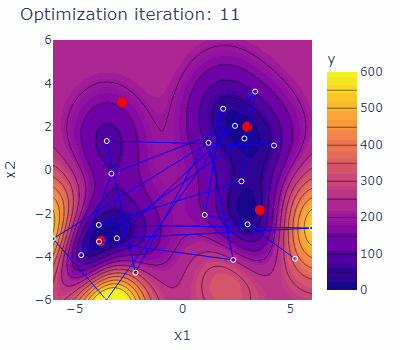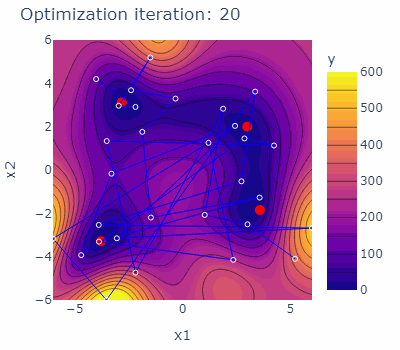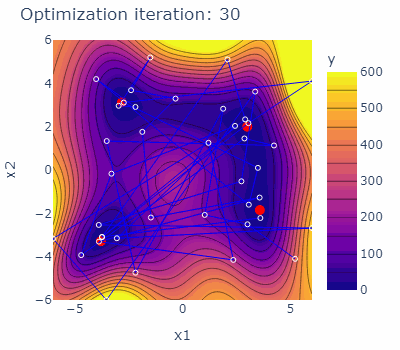
Let us consider a test function for single-objective optimization - the Himmelblau's function. The Himmelblau's function has four identical local minima used to test the performance of optimization algorithms. The optimization domain of the Himmelblau's function is illustrated below together with the four minima marked red.

Defining the optimization output

Let's consider the single continuous output variable y of the Himmelblau's function with the objective to minimize it. In BoFire's terminology, we create a MinimizeObjective object to define the optimization objective of a Continuous Output feature.

from bofire.data_models.features.api import ContinuousOutput
from bofire.data_models.objectives.api import MinimizeObjective


objective = MinimizeObjective()
output_feature = ContinuousOutput(key="y", objective=objective)

For more details on Output features and Objective objects, see the respective sections in our docs.

Defining the optimization inputs

For the two continuous input variables of the Himmelblau's function x1 and x2, we create two ContinuousInput features including boundaries following BoFire's terminology.

from bofire.data_models.features.api import ContinuousInput


input_feature_1 = ContinuousInput(key="x1", bounds=[-5, 5])
input_feature_2 = ContinuousInput(key="x2", bounds=[-5, 5])

For more details on Input features, see the respective sections in our docs.

Defining the optimization domain

In BoFire's terminology, Domain objects fully describe the search space of the optimization problem. Input and Output features are optionally bound with Constraint objects to specify allowed relationships between the parameters. Here, we will run an unconstrained optimization. For more details, see the respective sections in our docs.

from bofire.data_models.domain.api import Domain, Inputs, Outputs


domain = Domain(
    inputs=Inputs(features=[input_feature_1, input_feature_2]),
    outputs=Outputs(features=[output_feature]),
)

Draw candidates and execute experiments

Let's define the Himmelblau's function to evaluate points in the domain space.

def himmelblau(x1, x2):
    return (x1**2 + x2 - 11) ** 2 + (x1 + x2**2 - 7) ** 2

To initialize an iterative Bayesian optimization loop, let's first randomly draw 10 samples from the domain. In BoFire's terminology, those suggested samples are called Candidates.

candidates = domain.inputs.sample(10, seed=13)

print(candidates)

>           x1        x2
>  0  1.271053  1.649396
>  1 -5.012360 -1.907210
>  2 -4.541719  5.609014
>  3  ...       ...

Let's evaluate the function output for the randomly drawn candidates using the himmelblau function to obtain Experiments in BoFire's terminology.

experimental_output = candidates.apply(
    lambda row: himmelblau(row["x1"], row["x2"]), axis=1
)

experiments = candidates.copy()
experiments["y"] = experimental_output

print(experiments)

>           x1        x2           y
>  0  1.271053  1.649396   68.881387
>  1 -5.012360 -1.907210  219.383137
>  2 -4.541719  5.609014  628.921615
>  3 ...        ...       ...

For more details on candidates and experiments, see the respective sections in our docs.

Defining an optimization strategy

Let's specify the strategy how the Bayesian optimization campaign should be conducted. Here, we define a single-objective Bayesian optimization strategy and pass the optimization domain together with a acquisition function. Here, we use logarithmic expected improvement qLogEI as the acquisition function.

from bofire.strategies.api import SoboStrategy
from bofire.data_models.acquisition_functions.api import qLogEI

sobo_strategy = SoboStrategy.make(
    domain=domain, acquisition_function=qLogEI(), seed=19
)

It is possible to separate BoFire into serializable parameters and a functional part. We call the serializable parameters usually data models. This is especially helpful when working with REST APIs. See the respective sections in our docs.

Run the optimization loop

To run the optimization loop using BoFire's terminology, we first tell the strategy object about the experiments we have already executed.

sobo_strategy.tell(experiments=experiments)

We run the optimization loop for 30 iterations. In each iteration, we ask the strategy object to suggest one new candidate, which is returned as a list containing a single item. We then perform a new experiment by evaluating the Himmelblau function output of this candidate. After completing the experiment, we add the new data to our existing experiments and tell the strategy object about the updated dataset. This process is repeated for each of the 30 iterations.

for _ in range(30):
    new_candidates = sobo_strategy.ask(candidate_count=1)

    new_experiments = new_candidates.copy()
    new_experiments["y"] = new_candidates.apply(
        lambda row: himmelblau(row["x1"], row["x2"]), axis=1
    )

    sobo_strategy.tell(experiments=new_experiments)

The optimization behavior of the strategy is shown in the animated figure below. The four minima are marked red, the experiments carried out are marked blue with blue lines connecting them. The contours are indicating the predicted mean of the current model of each iteration.

Documentation

Documentation including a section on how to get started can be found under https://experimental-design.github.io/bofire/.

Reference

We would love for you to use BoFire in your work! If you do, please cite our paper:

@misc{durholt2024bofire,
  title={BoFire: Bayesian Optimization Framework Intended for Real Experiments},
  author={Johannes P. D{\"{u}}rholt and Thomas S. Asche and Johanna Kleinekorte and Gabriel Mancino-Ball and Benjamin Schiller and Simon Sung and Julian Keupp and Aaron Osburg and Toby Boyne and Ruth Misener and Rosona Eldred and Wagner Steuer Costa and Chrysoula Kappatou and Robert M. Lee and Dominik Linzner and David Walz and Niklas Wulkow and Behrang Shafei},
  year={2024},
  eprint={2408.05040},
  archivePrefix={arXiv},
  primaryClass={cs.LG},
  url={https://arxiv.org/abs/2408.05040},
}

Bayesian optimization in BoFire is based on META's BoTorch library. For BoTorch, please cite also the botorch paper:

@inproceedings{NEURIPS2020_f5b1b89d,
    author = {Balandat, Maximilian and Karrer, Brian and Jiang, Daniel and Daulton, Samuel and Letham, Ben and Wilson, Andrew G and Bakshy, Eytan},
    booktitle = {Advances in Neural Information Processing Systems},
    editor = {H. Larochelle and M. Ranzato and R. Hadsell and M.F. Balcan and H. Lin},
    pages = {21524--21538},
    publisher = {Curran Associates, Inc.},
    title = {BoTorch: A Framework for Efficient Monte-Carlo Bayesian Optimization},
    url = {https://proceedings.neurips.cc/paper_files/paper/2020/file/f5b1b89d98b7286673128a5fb112cb9a-Paper.pdf},
    volume = {33},
    year = {2020}
}

For molecular optimizations, BoFire uses the molecular kernels from the Gauche library. If you use the molecular kernels in BoFire please cite also the gauche paper:

@inproceedings{NEURIPS2023_f2b1b2e9,
    author = {Griffiths, Ryan-Rhys and Klarner, Leo and Moss, Henry and Ravuri, Aditya and Truong, Sang and Du, Yuanqi and Stanton, Samuel and Tom, Gary and Rankovic, Bojana and Jamasb, Arian and Deshwal, Aryan and Schwartz, Julius and Tripp, Austin and Kell, Gregory and Frieder, Simon and Bourached, Anthony and Chan, Alex and Moss, Jacob and Guo, Chengzhi and D\"{u}rholt, Johannes Peter and Chaurasia, Saudamini and Park, Ji Won and Strieth-Kalthoff, Felix and Lee, Alpha and Cheng, Bingqing and Aspuru-Guzik, Alan and Schwaller, Philippe and Tang, Jian},
    booktitle = {Advances in Neural Information Processing Systems},
    editor = {A. Oh and T. Naumann and A. Globerson and K. Saenko and M. Hardt and S. Levine},
    pages = {76923--76946},
    publisher = {Curran Associates, Inc.},
    title = {GAUCHE: A Library for Gaussian Processes in Chemistry},
    url = {https://proceedings.neurips.cc/paper_files/paper/2023/file/f2b1b2e974fa5ea622dd87f22815f423-Paper-Conference.pdf},
    volume = {36},
    year = {2023}
}

Contributing

See our Contributing guidelines. If you are not sure about something or find bugs, feel free to create an issue.

By contributing you agree that your contributions will be licensed under the same license as BoFire: BSD 3-Clause License.

Versioning

Starting with release 0.1.0, we follow a pragmatic versioning scheme.

BIGRELEASE.MAJOR.MINOR

Thereby, BIGRELEASE and MAJOR releases can contain breaking changes to our public API. Vice versa, every breaking change of our API is at least a MAJOR release.