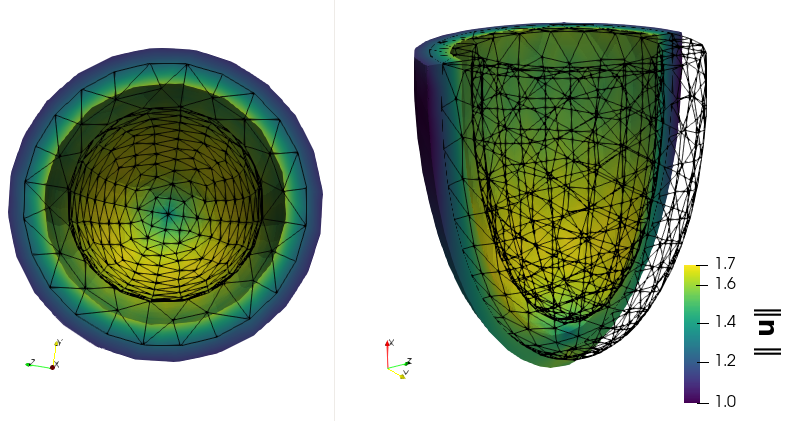
fenicsx-pulse

fenicsx-pulse is a cardiac mechanics solver based on FEniCSx. It is a successor of pulse which is a cardiac mechanics solver based on FEniCS.

• Documentation: https://finsberg.github.io/fenicsx-pulse/
• Source code: https://github.com/finsberg/fenicsx-pulse

Install

You can install the library with pip

python3 -m pip install fenicsx-pulse

or with conda

conda install -c conda-forge fenicsx-pulse

Note that installing with pip requires FEniCSx already installed

We also provide a pre-built docker image with FEniCSx and fenicsx_pulse installed. You pull this image using the command

docker pull ghcr.io/finsberg/fenicsx-pulse:v0.5.1

Getting started

Here is a minimal example of how to use fenicsx-pulse to solve a simple cardiac mechanics problem.

import numpy as np
import dolfinx
import cardiac_geometries
import pulse

# Create a geometry with cardiac-geometries
geo = cardiac_geometries.mesh.lv_ellipsoid(
    outdir="geometry",
    create_fibers=True,
    fiber_space="Quadrature_6",
)
# Convert the geometry to a pulse.Geometry
geometry = pulse.HeartGeometry.from_cardiac_geometries(geo, metadata={"quadrature_degree": 6})

# Create a material model
material_params = pulse.HolzapfelOgden.transversely_isotropic_parameters()
material = pulse.HolzapfelOgden(f0=geo.f0, s0=geo.s0, **material_params)

# Define model for active contraction
Ta = pulse.Variable(dolfinx.fem.Constant(geometry.mesh, dolfinx.default_scalar_type(0.0)), "kPa")
active_model = pulse.ActiveStress(geo.f0, activation=Ta)

# Define mode for compressibility
comp_model = pulse.Incompressible()

# Assemble into a cardiac model
model = pulse.CardiacModel(
    material=material,
    active=active_model,
    compressibility=comp_model,
)

# Define boundary conditions
traction = pulse.Variable(
    dolfinx.fem.Constant(geometry.mesh, dolfinx.default_scalar_type(0.0)), "kPa"
)
neumann = pulse.NeumannBC(traction=traction, marker=geometry.markers["ENDO"][0])


def dirichlet_bc(V: dolfinx.fem.FunctionSpace):
    # Find facets for the BASE marker
    facets = geo.ffun.find(geo.markers["BASE"][0])
    # Locate degrees of freedom for the x-component (sub(0)) on these facets
    dofs = dolfinx.fem.locate_dofs_topological(V.sub(0), geo.mesh.topology.dim - 1, facets)
    # Return the Dirichlet BC object
    return [dolfinx.fem.dirichletbc(0.0, dofs, V.sub(0))]


robin_epi = pulse.RobinBC(
    value=pulse.Variable(
        dolfinx.fem.Constant(geometry.mesh, dolfinx.default_scalar_type(1e3)),
        "Pa / m",
    ),
    marker=geometry.markers["EPI"][0],
)
robin_base = pulse.RobinBC(
    value=pulse.Variable(
        dolfinx.fem.Constant(geometry.mesh, dolfinx.default_scalar_type(1e3)),
        "Pa / m",
    ),
    marker=geometry.markers["BASE"][0],
)

bcs = pulse.BoundaryConditions(neumann=(neumann,), dirichlet=(dirichlet_bc,), robin=(robin_base, robin_epi))

# Create a mechanics problem
problem = pulse.StaticProblem(
    model=model,
    geometry=geometry,
    bcs=bcs,
)
# Perform an initial solve
problem.solve()

# Create a file for storing the solution
vtx = dolfinx.io.VTXWriter(geometry.mesh.comm, "displacement.bp", [problem.u], engine="BP4")
vtx.write(0.0)

# Assign a pressure and activation and ramp them up in steps
target_pressure = 5.0  # kPa
target_activation = 5.0  # kPa
num_steps = 5
for i, (pressure, activation) in enumerate(
    zip(np.linspace(0, target_pressure, num_steps), np.linspace(0, target_activation, num_steps))
):
    traction.assign(pressure)  # kPa
    Ta.assign(activation)  # kPa
    problem.solve()
    # Save the displacement field
    vtx.write(i + 1)
vtx.close()

A more realistic example is visualized here:

u_simulation_warped.mp4

Checkout out the demos in the documentation for more examples.

Contributing

See https://finsberg.github.io/fenicsx-pulse/CONTRIBUTING.html